
【题目】已知关于x的一元二次方程x2+2mx+m2-1=0.
(1)不解方程,判别方程的根的情况;
(2)若方程有一个根为3,求m的值.
【答案】
(1)解:由题意得,a=1,b=2m,c=m2﹣1,
∵△=b2﹣4ac=(2m)2﹣4×1×(m2﹣1)=4>0,
∴方程x2+2mx+m2﹣1=0有两个不相等的实数根
(2)解:∵x2+2mx+m2﹣1=0有一个根是3,
∴32+2m×3+m2﹣1=0,
解得,m1=﹣4或m2=﹣2
【解析】(1)求出方程的判别式,![]() >0,有两个不相等的实数根;(2)利用根的定义,代入方程,即可求出m值.
>0,有两个不相等的实数根;(2)利用根的定义,代入方程,即可求出m值.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
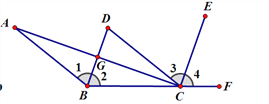
【题目】如图,CD//AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同.甲、乙两人每天共加工35个零件,设甲每天加工x个A型零件.
(1)直接写出乙每天加工的零件个数;(用含x的代数式表示)
(2)求甲、乙每天各加工零件多少个?
(3)根据市场预测,加工A型零件所获得的利润为m元/件(3≤m≤5),加工B型零件所获得的利润每件比A型少1元.求甲、乙每天加工的零件所获得的总利润P(元)与m的函数关系式,并求P的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.

(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全,小明骑单车上学,当他骑了一段时,想起要买文具,于是又折回到刚经过的文具店,买到文具后继续去学校,下图是他本次所用的时间与离家路程的关系示意图,根据图中提供的信息回答下列问题:

(1)小明家到学校的路程是___________米;小明在文具店停留了__________分钟.
(2)本次上学途中,小明一共行驶了多少米?
(3)我们认为骑单车的速度超过300米/分钟就超越了安全限度,问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气对人们健康的影响,市场上的空气净化器成了热销产品.某公司经销一种空气净化器,每台净化器的成本价为200元.经过一段时间的销售发现,每月的销售量y(台)与销售单价x(元)的关系为y=-2x+1000.
(1)该公司每月的利润为w元,写出利润w与销售单价x的函数关系式;
(2)若要使每月的利润为40000元,销售单价应定为多少元?
(3)公司要求销售单价不低于250元,也不高于400元,求该公司每月的最高利润和最低利润分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形 ABCD 中,放入六个形状大小相同的长方形,所标尺寸如图所示, 则图中阴影部分面积为( )

A. 44cm2B. 36cm2C. 96 cm2D. 84cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,在
中,在![]() 边上取两点
边上取两点![]() 、
、![]() ,使
,使![]() .若
.若![]() ,
,![]() ,
,![]() , 则以
, 则以![]() ,
,![]() ,
,![]() 为边长的三角形的形状为( )
为边长的三角形的形状为( )

A.锐角三角形B.直角三角形C.钝角三角形D.随![]() ,
,![]() ,
,![]() 的值而定
的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰Rt△CEF的斜边CE在正方形ABCD的边BC的延长线上,CF>BC,取线段AE的中点M 。
(1)求证:MD=MF,MD⊥MF
(2)若Rt△CEF绕点C顺时针旋转任意角度(如图2),其他条件不变。(1)中的结论是否仍然成立,若成立,请证明,若不成立,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com