
����Ŀ����ͼ��1������A��B��C���ֲ�ͬ�ͺŵĿ�Ƭ�����ţ�����A���DZ߳�Ϊa��a��b���������Σ�B���dz�Ϊa����Ϊb�ij����Σ�C���DZ߳�Ϊb�������Σ�

��1������A�Ϳ�Ƭ1�ţ�B�Ϳ�Ƭ2�ţ�C�Ϳ�Ƭ1��ƴ����һ�������Σ���ͼ��2�������������εı߳�Ϊ�� �������ݸ�ͼ����д��һ��������ʽ�ֽ�ĵ�ʽ���� ����
��2����Ҫƴһ����Ϊ2a+b����Ϊa+2b�ij����Σ�����ҪA�Ƭx�ţ�B�Ƭy�ţ�C�Ƭz�ţ���x+y+z���� ����
��3������A�Ϳ�Ƭ1�ţ�B�Ϳ�Ƭ6�ţ�C�Ϳ�Ƭ11�ţ�����18�ſ�Ƭ���õ����ſ�Ƭ�����µĿ�Ƭȫ���ϣ�����ƴ��һ�������λ����������м���ƴ��������ͨ������˵�����ɣ�
���𰸡���1��a+b��a2+2ab+b2����a+b��2����2��9����3������ƴ������һ�֣�A�Ϳ�Ƭ�õ�1�ţ�B�Ϳ�Ƭ�õ�1�ţ���ƴ��һ�������Σ��ڶ��֣�A�Ϳ�Ƭ�õ�1�ţ�C�Ϳ�Ƭ�õ�1�ţ���ƴ��һ�������Σ����������2��ƴ���������֣�C�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ�
��������
��1����ͼ�ɵÿɵ������εı߳�Ϊ![]() ����ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽ
����ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽ![]() ��
��
��2����Ϊ![]() ��������Ҫ��
��������Ҫ��![]() �Ƭ2�ţ�
�Ƭ2�ţ�![]() �Ƭ5�ţ�
�Ƭ5�ţ�![]() �Ƭ2�ţ�������
�Ƭ2�ţ�������![]() ��
��![]() ��
��![]() ��Ӧ��ֵ��
��Ӧ��ֵ��
��3����һ�֣�![]() �Ϳ�Ƭ�õ�1�ţ�
�Ϳ�Ƭ�õ�1�ţ�![]() �Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ
�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
�ڶ��֣�![]() �Ϳ�Ƭ�õ�1�ţ�
�Ϳ�Ƭ�õ�1�ţ�![]() �Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ
�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ![]() ����Ϊ
����Ϊ![]() ��
��
�����֣�![]() �Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�Ϊ
�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�Ϊ![]() ��
��
�⣺��1����ͼ��1����ͼ��2���ɵ������εı߳�Ϊ a+b��
��ͼ��2���ɵ���ʽ�ֽ�ĵ�ʽa2+2ab+b2����a+b��2��
�ʴ�Ϊa+b��a2+2ab+b2����a+b��2��
��2���ߣ�2a+b����a+2b����2a2+5ab+2b2��
����Ҫ��A�Ƭ2�ţ�B�Ƭ5�ţ�C�Ƭ2�ţ�
��x+y+z��2+5+2��9��
�ʴ�Ϊ9��
��3������ƴ����
��һ�֣�A�Ϳ�Ƭ�õ�1�ţ�B�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ5A+11b����Ϊb��
��b��5a+11b����5ab+11b2��
�ڶ��֣�A�Ϳ�Ƭ�õ�1�ţ�C�Ϳ�Ƭ�õ�1�ţ�����ƴ��һ�������Σ��������εij�Ϊ3A+5b����Ϊ2b��
��2b��3a+5b����6ab+10b2�����߳�Ϊ6A+10b����Ϊb���ࣨ6a+10b��b��6ab+10b2�����������2��ƴ����
�����֣�C�Ϳ�Ƭ�õ�2�ţ�����ƴ��һ�������η��Σ��������α߳�ΪA+3b��
�ࣨa+3b��2��a2+6ab+9b2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ͼ
��ͼ![]() ���߶�
���߶�![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ���ŵ�
��ʼ���ŵ�![]() ��
��![]() ���ٶ�˳ʱ����תһ�ܻص���
���ٶ�˳ʱ����תһ�ܻص���![]() ��ֹͣ����
��ֹͣ����![]() ͬʱ����������
ͬʱ����������![]() ��
��![]() ����
����![]() ���˶�������
���˶�������![]() ��
��![]() ������ǡ�����������
������ǡ�����������![]() �˶����ٶ�Ϊ________
�˶����ٶ�Ϊ________![]() ��
��

![]() ��һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���
��һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���![]() ����ͼ��ʽ������һ�����У�
����ͼ��ʽ������һ�����У�![]() ��
��![]() ��
��![]() ��
��![]() ���������dz�
���������dz�![]() �̶�����һ���dz�
�̶�����һ���dz�![]() ��
��![]() �ߴ�
�ߴ�![]() �߿�ʼ�Ƶ�
�߿�ʼ�Ƶ�![]() ת����ת���ٶ���
ת����ת���ٶ���![]() ����
����![]() ���ٶ���ͬ����
���ٶ���ͬ����![]() �ҵ�
�ҵ�![]() ��ֱ��
��ֱ��![]() ���Ϸ�ʱ�����������dz��Ƿ����һ�����ƽ�У������ڣ���д��
���Ϸ�ʱ�����������dz��Ƿ����һ�����ƽ�У������ڣ���д��![]() �п��ܵ�ֵ����Ӧת����ʱ�䣻�������ڣ���˵�����ɣ�
�п��ܵ�ֵ����Ӧת����ʱ�䣻�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵���������Ʒ�Ƶļ�����������2��AƷ�ƺ�3��BƷ�Ƶļ���������280Ԫ������3��AƷ�ƺ�1��BƷ�Ƶļ���������210Ԫ��
��������������Ʒ�Ƽ������ĵ��ۣ�
��������ѧǰ�����̵�������ּ�������չ�˴����������취���£�AƷ�Ƽ�������ԭ�۵ľ������ۣ�BƷ�Ƽ�����10�����ϳ������ְ�ԭ�۵��������ۣ��蹺��x��AƷ�Ƶļ�������Ҫy1Ԫ������x��BƷ�Ƶļ�������Ҫy2Ԫ���ֱ����y1��y2����x�ĺ�����ϵʽ��
������ijУ�����幺��ͬһƷ�Ƶļ����������������������������15������������Ʒ�Ƶļ����������㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MON��30������A1��A2��A3����������ON�ϣ���B1��B2��B3����������OM�ϣ���A1B1B2����A2B2B3����A3B3B4������Ϊ�ȱ������Σ���OB1��1������A8B8B9�ı߳�Ϊ��������
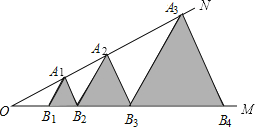
A.64B.128C.132D.256
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ĵ�����������Ŀ纣���ţ�������۴���ɽ�����Ű뵺�㶫ʡ�麣�У������麣վ�����վȫ��Լ55ǧ�ף�2018��10��24������9ʱ��ʽͨ����һ���۹��ʿ���麣վ������25���Ӻ�һ��С������ͬһ�ص���������ͬʱ�������վ����֪С�������ٶ��ǹ۹��ʿ��1.6������۹��ʿ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+��2��a��x��2��a��0����ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C���������н��ۣ�
����a��0�������£�����aȡ��ֵ����A��һ�����㣻
����a��0�������£�����aȡ��ֵ�������ߵĶԳ���һ��λ��y�����ࣻ
��y����Сֵ�����ک�2��
����AB=AC����a=![]() ��
��
������ȷ�Ľ����У�����������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ڽ��ڡ�O��BC��ֱ��AD�ڵ�E������C��AD�Ĵ��߽�AB���ӳ����ڵ�G������ΪF������OC��
��1������G=48�㣬���ACB�Ķ�����
��2����AB=AE����֤����BAD=��COF��
��3������2���������£�����OB�����AOB�����ΪS1����ACF�����ΪS2����tan��CAF=![]() ����
����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��1������֪������ABC�У���BAC=90����AB=AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E����֤��DE=BD+CE��
��2����ͼ��2��������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=����������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ��������������������֤����������������˵�����ɣ�
��3����ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA=��AEC=��BAC����֤:��DEF�ǵȱ������Σ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�״����������һ��������ʱ�������������õ���Ƶ���ֲ�����δ��ɣ���
���ݶ� | 30��40 | 40��50 | 50��60 | 60��70 | 70��80 | �ܼ� |
Ƶ �� | 10 | 40 | | | 20 | |
�ٷֱ� | 5% | | 40% | | 10% | |
ע��30��40Ϊʱ�ٴ��ڵ���30ǧ��С��40ǧ�ף�������ͬ��
��1������ѱ��е�������д������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�������·������ʱ�ٳ���60ǧ��ΪΥ�£���Υ�³������ж�������
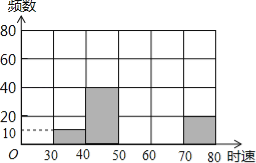
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com