
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
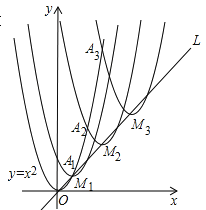
【答案】(4027,4027).
【解析】
试题解析:M1(a1,a1)是抛物线y1=(x-a1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x-a1)2+a1相交于A1,
得x2=(x-a1)2+a1,
即2a1x=a12+a1,
x=![]() (a1+1).
(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a2)是抛物线y2=(x-a2)2+a2=x2-2a2x+a22+a2顶点,
抛物线y=x2与y2相交于A2,
x2=x2-2a2x+a22+a2,
∴2a2x=a22+a2,
x=![]() (a2+1).
(a2+1).
∵x为整数点,
∴a2=3,
M2(3,3),
M3(a3,a3)是抛物线y2=(x-a3)2+a3=x2-2a3x+a32+a3顶点,
抛物线y=x2与y3相交于A3,
x2=x2-2a3x+a32+a3,
∴2a3x=a32+a3,
x=![]() (a3+1).
(a3+1).
∵x为整数点
∴a3=5,
M3(5,5),
∴点M2014,两坐标为:2014×2-1=4027,
∴M2014(4027,4027).


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
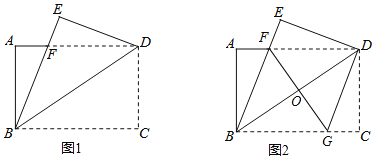
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
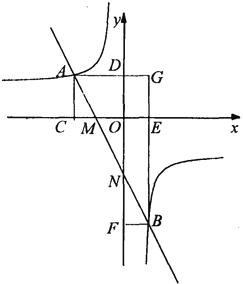
【题目】直线MN与x轴、y轴分别交于点M、N,并且经过第二、三、四象限,与反比例函数y=![]() (k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(k<0)的图象交于点A、B,过A、B两点分别向x轴、y轴作垂线,垂足为C、D、E、F,AD与BF交于G点.
(1)比较大小:S矩形ACOD S矩形BEOF(填“>,=,<”).
(2)求证:①AGGE=BFBG;
②AM=BN;
(3)若直线AB的解析式为y=﹣2x﹣2,且AB=3MN,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为方便市民出行,甲、乙两家公司推出专车服务,运价收费如下:设行驶路程![]() 时,用含
时,用含![]() 的代数式表示乙公司的运价.
的代数式表示乙公司的运价.
行驶路程 | 收费标准 | |
甲 | 乙 | |
不超过 | 起步价6元 | 起步价7元 |
超过 | 每公里2.1元 | 每公里1.6元 |
超出 | 每公里2.2元 | |
(1)当![]() 时,则费用表示为 元;当
时,则费用表示为 元;当![]() 时,则费用表示为 元.
时,则费用表示为 元.
(2)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?
(3)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个有50个奇数排成的数阵,用如图所示的框去框住四个数,并求出这四个数的和,在下列给出的备选答案中,有可能是这四个数的和的是( )
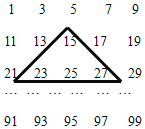
A. 114 B. 122 C. 220 D. 84
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如图:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离s(千米)与时间t(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点A(0,12),点B坐标为(m,0),曲线BC可用二次函数s=![]() t2+bt+c(b,c是常数)刻画.
t2+bt+c(b,c是常数)刻画.
(1)求m的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以0.48千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为0.48千米/分,小红逐渐落后.问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度v=v0+![]() (t﹣30),v0是加速前的速度).
(t﹣30),v0是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)求证:△ADC∽△CDB;
(2)若AC=2,AB=![]() CD,求⊙O半径.
CD,求⊙O半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
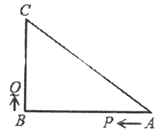
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中P点从点A开始沿AB方向运动且速度为每秒lcm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求线段PQ的长?
(2)当点Q在边BC上运动时,出发儿秒钟后,OPQB是等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com