
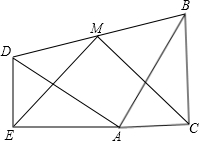
 如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.
如图,两个全等的含30°、60°角的三角板ADE和三角板ABC放置在一起,∠DEA=∠ACB=90°,∠DAE=∠ABC=30°,E、A、C三点在一条直线上,连接BD,取BD中点M,连接ME、MC,试判断△EMC的形状,并说明理由.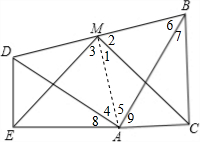 解:△EMC的形状是等腰直角三角形,
解:△EMC的形状是等腰直角三角形,| 1 |
| 2 |
|


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
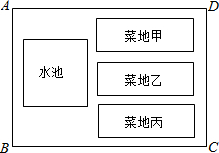 如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.
如图,矩形场地ABCD面积为234米2,其中有3块完全一样的矩形菜地和一个正方形水池,水池与AB边,水池与菜地,菜地与菜地,菜地甲与AD边,菜地丙与BC边,菜地与CD边之间的距离均为1米,且菜地长、宽、正方形水池边长之比为3:1:2,求该矩形场地ABCD的长BC及宽AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、方程没有整数根 |
| B、方程有两个相等的整数根 |
| C、方程有两个不相等的整数根 |
| D、不能判定方程整数根的情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、为了了解市民对重庆市创建全国环保模范城市的关注程度,王华在学校随机采访了8名初三学生 |
| B、为了了解学校学生参加课外活动的情况,张民同学在初三年级向3位好友做了调查 |
| C、为了了解“天宫一号”飞船零部件的状况,检测人员采用了普查的方式 |
| D、为了了解中央电视台2012年春节联欢晚会的收视率,统计人员采用了普查的方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
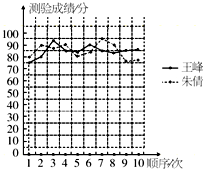 光华中学要选派一名学生去参加区级电脑知识竞赛,王峰和朱倩两位同学平时电脑都学的不错,为了确定谁去参赛,老师对他们的电脑知识进行了10次模拟测验,测验成绩情况如下面的折线统计图(如图):
光华中学要选派一名学生去参加区级电脑知识竞赛,王峰和朱倩两位同学平时电脑都学的不错,为了确定谁去参赛,老师对他们的电脑知识进行了10次模拟测验,测验成绩情况如下面的折线统计图(如图):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com