
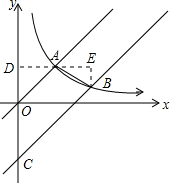
 如图,直线y=x与双曲线y=
如图,直线y=x与双曲线y=| 4 | x |
| 4 |
| x |
|
|
|
| 4 |
| x |
| 4 |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
| 7 |
| 2 |


科目:初中数学 来源: 题型:
 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=| 4 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
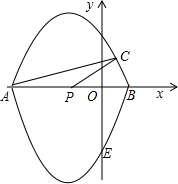 点,且P(-1,0),C(
点,且P(-1,0),C(| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:湖南省中考真题 题型:解答题


查看答案和解析>>
科目:初中数学 来源: 题型:
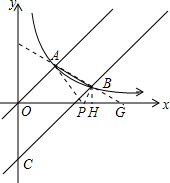
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=![]() 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).

1.发现C船时,A、B、C三船所在位置的坐标分别为A(_______,_______)、B(_______,_______)和C(_______,_______);
2.发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com