
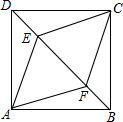
 正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.
正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.分析 (1)四边形AECF是菱形,根据对角线垂直的平行四边形是菱形进行判断.
(2)在RT△EOC中,利用勾股定理求出EC即可解决问题.
解答 解:(1)结论四边形AECF是菱形,
理由:如图,连接AC与BD交于点O,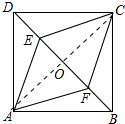
∵四边形ABCD是正方形,
∴OA=OC,OB=OD,AC⊥BD,
∵DE=BF,
∴OE=OF,OA=OC,
∴四边形AECF是平行四边形,∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵EF=6,DE=BF=1,
∴OE=OF=3,OC=OD=4,
在RT△EOC中,∵∠EOC=90°,EO=3,OC=4,
∴EC=$\sqrt{E{O}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∴菱形AECF的周长为4×5=20cm.
点评 本题考查菱形的判定和性质、正方形的性质、解题的关键是熟练掌握菱形的判定方法和性质,记住对角线垂直的平行四边形是菱形,学会常用辅助线的添加方法,属于中考常考题型.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
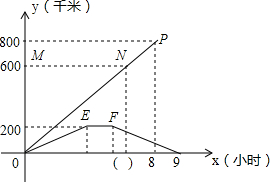 在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:
在笔直的公路上依次有A,B,C三地,甲车从A地出发速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地停留1小时后,按原速返回到C地,在两车行驶的过程中,甲、乙两车距各自出发的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示,请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
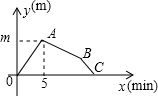
 甲、乙两人分别从A、B两地同时出发,甲到达B地后立即原速返回A地,共用了20分钟,又过5分钟后乙也到达A地,如图为甲、乙两人距B地的路程y(米)与行使时间x(分钟)之间的函数图象.
甲、乙两人分别从A、B两地同时出发,甲到达B地后立即原速返回A地,共用了20分钟,又过5分钟后乙也到达A地,如图为甲、乙两人距B地的路程y(米)与行使时间x(分钟)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
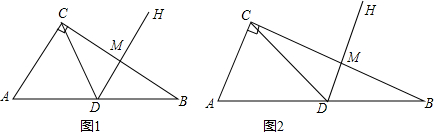
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4a2+4a+1=(2a+1)2 | B. | a2-4b2=(a-4b)(a+b) | C. | a2-2a-1=(a-1)2 | D. | (a-b)(a+b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
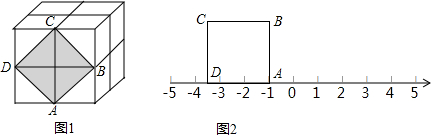
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com