【题目】如图，已知
， 
， 
，试说明：BE∥CF．
完善下面的解答过程，并填写理由或数学式：
解：∵ 
（已知）
∴AE∥ （ ）
∴
（ ）
∵
（已知）
∴
（ ）
∴DC∥AB（ ）
∴
（ ）
即
∵
（已知）
∴
（ ）
即
∴BE∥CF（ ） ．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴上，且点A坐标为（0，4），BC在x轴正半轴上，点C在B点右侧，反比例函数
（x＞0）的图象分别交边AD，CD于E，F，连结BF，已知，BC=k，AE=
CF，且S四边形ABFD=20，则k= _________．
[Failed to download image : http://192.168.0.10:8086/QBM/2019/1/17/2120855162306560/2123559773659136/STEM/85e8312ee4314e6b84d61ad733d78d14.png]
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，矩形OABC在平面直角坐标系内的位置如图所示，点O为坐标原点，点A的坐标示为(10，0)，点B的坐标为(10，8) ．
(1)直接写出点C的坐标为：C( ____ ，_____)；
(2)已知直线AC与双曲线y=
(m≠0)在第一象限内有一点交点Q为(5，n)，
①求m及n的值；
②若动点P从A点出发，沿折线AO→OC→CB的路径以每秒2个单位长度的速度运动，到达B处停止，△APQ的面积为S，当t取何值时，S=10．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，∠ABC=90°，∠CAB=∠CAD=22.5°，E在AB上，且∠DCE=67.5°，DE⊥AB于E，若AE=1，线段BE的长为____________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某旅客携带x kg的行李乘飞机，登机前，旅客可选择托运或快递行李，托运费y1（元）与行李重量x kg的对应关系由如图所示的一次函数图象确定，下表列出了快递费y2（元）与行李重量x kg的对应关系
(1) 如果旅客选择托运，求可携带的免费行李的最大重量为多少kg？
(2) 如果旅客选择快递，当1＜x≤15时，直接写出快递费y2（元）与行李的重量x kg之间的函数关系式
(3) 某旅客携带25kg的行李，设托运m kg行李（10≤m＜24，m为正整数），剩下的行李选择快递．当m为何值时，总费用y的值最小？并求出其最小值是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，若CO⊥AB，垂足为O，OE、OF分别平分∠AOC与∠BOC．求∠EOF的度数；
（2）如图2，若∠AOC=∠BOD=80°，OE、OF分别平分∠AOD与∠BOC．求∠EOF的度数；
（3）若∠AOC=∠BOD=α，将∠BOD绕点O旋转，使得射线OC与射线OD的夹角为β，OE、OF分别平分∠AOD与∠BOC．若α+β≤180°，α＞β，则∠EOC= ．（用含α与β的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
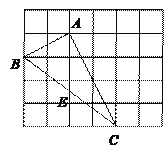
【题目】如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：
（1）画线段AD∥BC且使AD=BC，连接CD；
（2）线段AC的长为_______，CD的长为______，AD的长为________；
（3）四边形ABCD的面积为________.
查看答案和解析>>
科目：初中数学 来源： 题型：
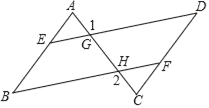
【题目】在括号内注明说理依据．如图已知∠B=∠D，∠1=∠2，试猜想∠A与∠C的大小关系，并说明理由．
解：猜想∠A=∠C
∵∠1=∠2 （已知）
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D （等量代换）
∴AB∥CD
∴∠A=∠C ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
