
分析 (1)根据零指数幂的意义、负整数指数幂的意义,特殊角的锐角三角函数值即可求出答案.
(2)根据分式的运算法则即可求出答案.
解答 解:(1)原式=1+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-3+2
=1+1-3+2
=1
(2)原式=$\frac{x+1}{x+2}÷\frac{{{{({x+1})}^2}}}{x+2}$
=$\frac{x+1}{x+2}×\frac{x+2}{{{{({x+1})}^2}}}=\frac{1}{x+1}$.
当$x=\sqrt{3}-1$时,
原式=$\frac{1}{{\sqrt{3}-1+1}}=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$.
点评 本题考查学生的运算能力,解题的关键熟练运用运算法则,本题属于基础题型.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
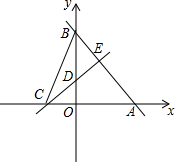 如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.
如图,直线y=-$\frac{4}{3}$x+8分别交x轴、y轴于A,B两点.线段AB的垂直平分线分别交x轴、y轴于C,D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
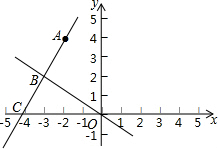 如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)
如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(-2,4),且与正比例函数y=-$\frac{2}{3}$x的图象交于点B(m,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.
(1)如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求:∠ABF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抽取前100名学生的成绩 | B. | 抽取后100名学生的成绩 | ||
| C. | 抽取(1)(2)两个班的学生成绩 | D. | 抽取学号为4的倍数的学生的成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
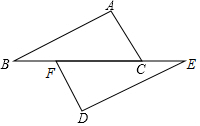 如图,已知点B、F、C、E在同一条直线上,AB∥DE,且AB=DE,∠A=∠D.
如图,已知点B、F、C、E在同一条直线上,AB∥DE,且AB=DE,∠A=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
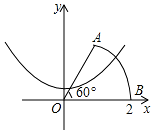 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴建立平面直角坐标系,点B的坐标为(2,0),扇形的圆心角是60°.若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是( )| A. | -4<k<$\frac{3}{4}$ | B. | -2<k<$\frac{3}{4}$ | C. | -4<k<$\sqrt{3}$-1 | D. | -2<k<$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com