
| A. | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | B. | 32、42、52 | C. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D. | 3k、4k、5k(k≠0) |
分析 根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形判定则可.
解答 解:A、($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,不能构成直角三角形,故此选项错误;
B、(32)2+(42)2≠(52)2,不能构成直角三角形,故此选项错误;
C、($\frac{1}{4}$)2+($\frac{1}{5}$)2≠($\frac{1}{3}$)2,不能构成直角三角形,故此选项错误;
D、(3k)2+(4k)2=(5k)2,能构成直角三角形,故此选项正确.
故选D
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
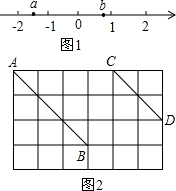
 (1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上);
(1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;
(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com