
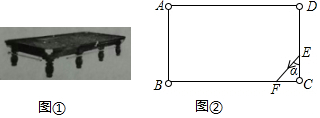
分析 根据球的运动轨迹可知四个三角形相似,并且相对的两个三角形全等,由于DE=4,CE=2,设CF=x,则BF=6$\sqrt{3}$-x,由△BGF∽△CEF,可得$\frac{BG}{EC}$=$\frac{BF}{FC}$,列出方程即可解决问题.
解答 解:如图:
∵DE=4,CE=2,球从E点出发,与DC夹角为α,经过BC、AB、AD三次反弹后回到E点,
∴四个三角形相似,并且相对的两个三角形全等,设CF=x,则BF=6$\sqrt{3}$-x,
∵△BGF∽△CEF,
∴$\frac{BG}{EC}$=$\frac{BF}{FC}$,
∴$\frac{4}{2}$=$\frac{6\sqrt{3}-x}{x}$,
∴x=2$\sqrt{3}$,
∴EF=$\sqrt{E{C}^{2}+C{F}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{2}^{2}}$=4.
故答案为4.
点评 考查了解直角三角形的应用,解题的关键是根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
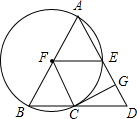 如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.
如图,在△ABD中,AB=AD,以AB为直径的⊙F交BD于点C,交AD于点E,CG⊥AD于点G,连接FE,FC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com