
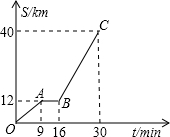
 如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题:分析 (1)直接利用总路程÷总时间=平均速度,进而得出答案;
(2)利用路程不发生变化时,即可得出停留的时间;
(3)利用待定系数法求出S与t的函数关系式,将S=30代入解析式求得t即可.
解答 解:(1)汽车在前9分钟内的平均速度是:$\frac{12}{9}$=$\frac{4}{3}$(km/min);
(2)汽车在中途停了:16-9=7(分钟);
(3)当16≤t≤30时,
则设S与t的函数关系式为:S=kt+b,
将(16,12),(30,40)代入得:$\left\{\begin{array}{l}{16k+b=12}\\{30k+b=40}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-20}\end{array}\right.$,
故当16≤t≤30时,S与t的函数关系式为:S=2t-20;
当S=30时,则30=2t-20,
解得t=25(分钟)
答:汽车行驶30千米的时间是25分钟.
点评 此题主要考查了一次函数的应用,利用数形结合得出点的坐标是解题关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:填空题
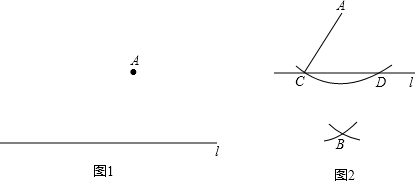
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
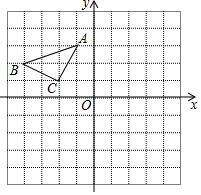 已知△ABC在平面直角坐标系中的位置如图所示.
已知△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
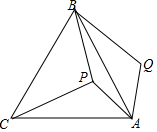 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=150°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
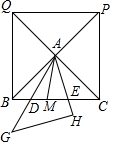 如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.
如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
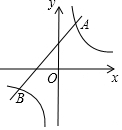 如图,已知点A(2,a),B(-4,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知点A(2,a),B(-4,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com