解:(1)根据三角形的三边关系,得
2<BC<12,
又BC是能被3整除的偶数,则BC=6cm.
∴这个三角形的周长=6+7+5=18cm.
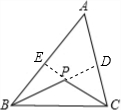
(2)a:延长CP交AB于点E,延长BP交AC于点D.
∵BP、CP分别是△ABC的角平分线
∴∠ABD=∠CBD,∠ACE=∠ECB;
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠CBD+2∠ECB=180°;
∵∠A=50°,
∴∠CBD+∠ECB=65°;
在△BPC中,
又∵∠BPC+∠CBP+∠PCB=180°,
∴∠BPC=115°.
b:同理∵∠A=n°,
∴∠CBD+∠ECB=
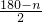
°;
在△BPC中,
又∵∠BPC+∠CBP+∠PCB=180°,
∴∠BPC=(180-
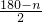
)°=(90+
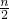
)°.
分析:(1)根据三角形的三边关系求得第三边的取值范围,再进一步结合已知BC是能被3整除的偶数和已知的两条边,求得第三边的值,即可解答;
(2)延长CP交AB于点E,延长BP交AC于点D.在△ABC中,根据角平分线的定义及三角形内角和定理,先求得∠ABD+∠ACE的值,从而求得∠CBD+∠ECB的值;然后在△BPC中利用三角形内角和定理求得∠BPC度数.
点评:本题考查三角形的三边关系、内角和定理及角平分线的性质,解答本题时要灵活运用所学的知识.

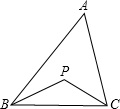 如图,在△ABC中.
如图,在△ABC中. 解:(1)根据三角形的三边关系,得
解:(1)根据三角形的三边关系,得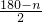 °;
°;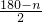 )°=(90+
)°=(90+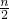 )°.
)°.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为