
【题目】如图,已知正方形ABCD中,E、F分别是正方形AD、CD边上的点,且∠EBF=45°,对角线AC交BE,BF于M,N,对于以下结论,正确的是( )①AE+CF=FE②△ABE≌△BCF③AM2+CN2=MN2④△EFD的周长等于2AB

A.①②③B.①②④C.①③④D.①②③④
【答案】C
【解析】
延长DA至点H,使AH=CF,连接BH,证明△BCF≌△BAH,△HBE≌△FBE即可判断①②④,然后作BG⊥EF,连接MG,NG,证明△BAM≌△BGM,△BCN≌△BGN,根据勾股定理即可判定③.
解:延长DA至点H,使AH=CF,连接BH,
∵四边形ABCD为正方形,
∴AB=BC,∠BAH=∠BCF=90°,
在△BCF和△BAH中
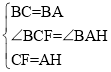
∴△BCF≌△BAH(SAS),
∴BF=BH,∠CBF=∠ABH,CF=AH,
∵∠EBF=45°,
∴∠ABE+∠CBF=45°,则∠HBE=45°,
在△HBE和△FBE中
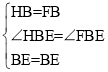
∴△HBE≌△FBE(SAS),
∴HE=HF,即CF+AE=EF,故①正确;
∵题上没有说明AE=CF,故②错误;
△EFD的周长=ED+EF+FD=ED+AE+CF+FD=2AB,故④正确;
作BG⊥EF,连接MG,NG,
∵△HBE≌△FBE,
∴∠BEA=∠BEG,从而得到△BAE≌△BGE,△BCF≌△BGF,
∴∠ABE=∠GBE,∠CBF=∠GBF,从而得到△BAM≌△BGM,△BCN≌△BGN,
∴AM=GM,CN=NG,∠BAM=∠BGM,∠BCN=∠BGN,
∵∠BAM+∠BCN=90°,
∴∠MGN=90°,
∴GM2+GN2=MN2
∴AM2+CN2=MN2,故③正确;
故正确的是①③④,故选C.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?

查看答案和解析>>
科目:初中数学 来源: 题型:
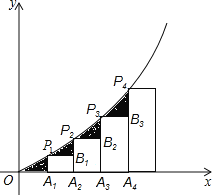
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=![]() x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
x2(x>0)的图象于点P1,P2,P3,…,Pn.若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对一种新型产品的产销情况进行了营销调查,发现年产量为x(吨)时,所需的成本y(万元)与(x2+60x+800)成正比例,投入市场后当年能全部售出且发现每吨的售价p(单位:万元)由基础价与浮动价两部分组成,其中基础价是固定不变的,浮动价与x成正比例,比例系数为-![]() .在营销中发现年产量为20吨时,所需的成本是240万元,并且年销售利润W(万元)的最大值为55万元.(注:年利润=年销售额-成本)
.在营销中发现年产量为20吨时,所需的成本是240万元,并且年销售利润W(万元)的最大值为55万元.(注:年利润=年销售额-成本)
(1)求y(万元)与x(吨)之间满足的函数解析式;
(2)求年销售利润W与年产量x(吨)之间满足的函数解析式;
(3)当年销售利润最大时,每吨的售价是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)
⑵当a=![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )
⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.

(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com