
���� ��1����д�С����ӡ�����ʯͷ���������ӡ����������Ŀ�Ƭ�����ֱ�Ϊ2��3��4��6��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��2���ɼ��������ˡ�ʯͷ�����������������ӡ�������ʤ��ֱ�����ø��ʹ�ʽ��⼴����ô𰸣�
��� �⣺��1����д�С����ӡ�����ʯͷ���������ӡ����������Ŀ�Ƭ�����ֱ�Ϊ2��3��4��6��
�������������������ʯͷ���ĸ����ǣ�$\frac{3}{2+3+4+6}$=$\frac{1}{5}$��
��2�����������ˡ�ʯͷ�����������������ӡ�������ʤ��
���һ�ʤ�ĸ����ǣ�$\frac{2+6}{2+3+4+6-1}$=$\frac{4}{7}$��
���� ���⿼���˸��ʹ�ʽ���õ���֪ʶ��Ϊ������=������������������֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 11 | B�� | -11 | C�� | $\frac{1}{11}$ | D�� | -$\frac{1}{11}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -1 | C�� | 1 | D�� | -$\frac{a}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | A | B�� | B | C�� | C | D�� | D |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | $\frac{1}{5}$ | C�� | ��5 | D�� | -$\frac{1}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪�߶�a��c����ͼ������ֱ�ߺ�Բ����Rt��ABC��ʹ��C=Rt�ϣ�BC=a��AB=c������ܰ���ѣ�1���뱣����ͼ�ۼ�������д������2�������ֱ�ߺ�Բ������������������ͼ��ʱ�������ǰ塢�������ȹ���ͼ������Ҳ�ɵ�5�֣�
��֪�߶�a��c����ͼ������ֱ�ߺ�Բ����Rt��ABC��ʹ��C=Rt�ϣ�BC=a��AB=c������ܰ���ѣ�1���뱣����ͼ�ۼ�������д������2�������ֱ�ߺ�Բ������������������ͼ��ʱ�������ǰ塢�������ȹ���ͼ������Ҳ�ɵ�5�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
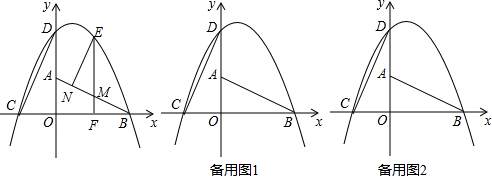
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+x=x2 | B�� | 2��x+1��=2x+1 | C�� | ��x+y��2=x2+y2 | D�� | x2•x=x3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com