
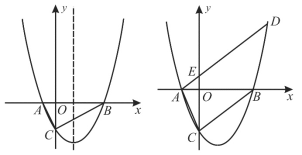
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(A点在B点的左边),与
两点(A点在B点的左边),与![]() 轴交于点
轴交于点![]() .
.
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,若以
在抛物线的对称轴上,若以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是平行四边形,求
、Q为顶点的四边形是平行四边形,求![]() 点的坐标;
点的坐标;
(3)如图2,过点![]() 作直线
作直线![]() 的平行线交抛物线于另一点
的平行线交抛物线于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() ﹕
﹕![]() =1﹕4. 求
=1﹕4. 求![]() 的值.
的值.
【答案】(1) ![]() ;(2)
;(2) ![]() 和
和![]()
![]() ;(3)
;(3) ![]()
【解析】
(1)设![]() ,
,![]() ,再根据根与系数的关系得到
,再根据根与系数的关系得到![]() ,根据勾股定理得到:
,根据勾股定理得到:![]() 、
、 ![]() ,根据
,根据![]() 列出方程,解方程即可;(2)求出A、B坐标,设出点Q坐标,利用平行四边形的性质,分类讨论点P坐标,利用全等的性质得出P点的横坐标后,分别代入抛物线解析式,求出P点坐标;
列出方程,解方程即可;(2)求出A、B坐标,设出点Q坐标,利用平行四边形的性质,分类讨论点P坐标,利用全等的性质得出P点的横坐标后,分别代入抛物线解析式,求出P点坐标;
(3)过点![]() 作DH⊥
作DH⊥![]() 轴于点
轴于点![]() ,由
,由![]() :
:![]() :
:![]() ,可得
,可得![]() :
:![]() :
:![]() .设
.设![]() ,可得
,可得 ![]() 点坐标为
点坐标为![]() ,可得
,可得![]() .设
.设![]() 点坐标为
点坐标为![]() .可证△
.可证△![]() ∽△
∽△![]() ,利用相似性质列出方程整理可得到
,利用相似性质列出方程整理可得到 ![]() ①,将
①,将![]() 代入抛物线上,可得
代入抛物线上,可得![]() ②,联立①②解方程组,即可解答.
②,联立①②解方程组,即可解答.
解:![]() 设
设![]() ,
,![]() ,则
,则![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() .
.
∵已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
∴![]()
在![]() △
△![]() 中:
中:![]() ,在
,在![]() △
△![]() 中:
中:![]() ,
,
∵△![]() 为直角三角形,由题意可知∠
为直角三角形,由题意可知∠![]() °,
°,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,
又![]() ,
,
∴![]() .
.
![]() 由
由![]() 可知:
可知:![]() ,令
,令![]() 则
则![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
①以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是四边形
、Q为顶点的四边形是四边形![]() 时,
时,
设抛物线的对称轴为![]() ,l与
,l与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥l,垂足为点
⊥l,垂足为点![]() ,
,
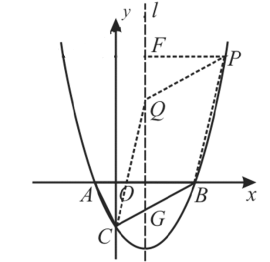
即∠![]() °
°![]() ∠
∠![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ∥
∥![]() ,又l∥
,又l∥![]() 轴,
轴,
∴∠![]() ∠
∠![]() =∠
=∠![]() ,
,
∴△![]() ≌△
≌△![]() ,
,
∴![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
∴![]()
即![]() 点坐标为
点坐标为![]() .
.
②当以![]() 为边,以点
为边,以点![]() 、
、![]() 、
、![]() 、Q为顶点的四边形是四边形
、Q为顶点的四边形是四边形![]() 时,
时,
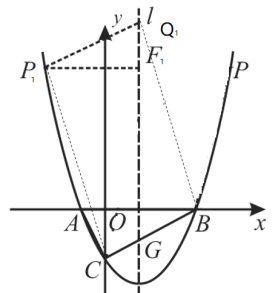
设抛物线的对称轴为![]() ,l与
,l与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ⊥l,垂足为点
⊥l,垂足为点![]() ,
,
即∠![]() °
°![]() ∠
∠![]() .
.
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ∥
∥![]() ,又l∥
,又l∥![]() 轴,
轴,
∴∠![]() ∠
∠![]() =∠
=∠![]() ,
,
∴△![]() ≌△
≌△![]() ,
,
∴![]() ,
,
∴![]() 点的横坐标为
点的横坐标为![]() ,
,
∴![]()
即![]() 点坐标为
点坐标为![]()
∴符合条件的![]() 点坐标为
点坐标为![]() 和
和![]() .
.
![]() 过点
过点![]() 作DH⊥
作DH⊥![]() 轴于点
轴于点![]() ,
,
∵![]() :
:![]() :
:![]() ,
,
∴![]() :
:![]() :
:![]() .
.
设![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,
∴![]() .
.
∵![]() 点在抛物线
点在抛物线![]() 上,
上,
∴![]() 点坐标为
点坐标为![]() ,
,
由(1)知![]() ,
,
∴![]() ,
,
∵![]() ∥
∥![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
∴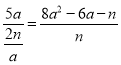 ,
,
即![]() ①,
①,
又![]() 在抛物线上,
在抛物线上,
∴![]() ②,
②,
将代入①得:![]() ,
,
解得![]() (舍去),
(舍去),![]()
把![]() 代入②得:
代入②得:![]() .
.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】一组数据7,2,5,4,2的方差为a,若再增加一个数据4,这6个数据的方差为b,则a与b的大小关系是( )
A. a>b B. a=b C. a<b D. 以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
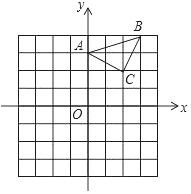
【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).
(1)作出△ABC绕点A顺时针方向旋转90°后得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并直接写出B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
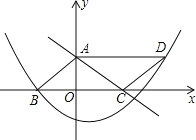
【题目】如图,点A、C分别是一次函数y=﹣![]() x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=
x+3的图象与y轴、x轴的交点,点B与点C关于原点对称,二次函数y=![]() x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
x2+bx+c的图象经过点B,且该二次函数图象上存在一点D,使四边形ABCD能构成平行四边形.
(1)求二次函数的表达式;
(2)动点P从点A到点D,同时动点Q从点C到点A都以每秒1个单位的速度运动,设运动时间为t秒.
①当t为何值时,有PQ丄AC?
②当t为何值时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E、F分别为AB、BC、AC的中点,则下列结论:①△ADF≌△FEC;②四边形ADEF为菱形;③![]() 。其中正确的结论是____________.(填写所有正确结论的序号)
。其中正确的结论是____________.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的汉字书写能力,某学校连续举办了几届汉字听写大赛,今年经过层层选拔,确定了参加决赛的选手,决赛的比赛规则是每正确听写出1个汉字得2分,满分是100分,下面是根据决赛的成绩绘制出的不完整的频数分布表、扇形统计图和频数分布直方图.
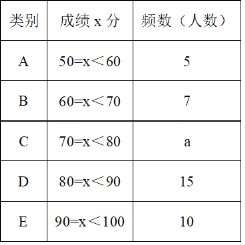
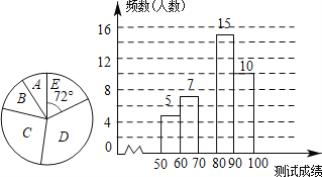
请结合图表完成下列各题
(1)表中a的值为______,并把频数分布直方图补充完整;
(2)学校想利用频数分布表估计这次决赛的平均成绩,请你直接写出平均成绩;
(3)通过与去年的决赛成绩进行比较,发现今年各类人数的中位数有了显著提高,提高了15%以上,求去年各类人数的中位数最高可能是多少?
(4)想从A类学生的3名女生和2名男生中选出两人进行培训,直接写出选中1名男生和1名女生的概率是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书籍是人类进步的阶梯,联合国教科文组织把每年的4月23日确定为“世界读书日”,某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数 | 43 | 31 | 15 | 5 | 4 | 2 |
请你根据以上信息解答下列问题:
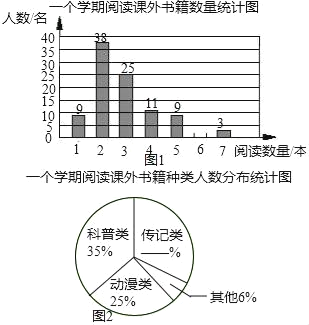
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有1200名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图像与直线
的图像与直线![]() 交于点
交于点![]() ,直线
,直线![]() 分别交x轴,y轴于C、B两点.
分别交x轴,y轴于C、B两点.
(1)求![]() 的值;
的值;
(2)已知点![]() ,当点P在函数
,当点P在函数![]() 的图像上时,求△POA的面积;
的图像上时,求△POA的面积;
(3)点Q在函数![]() 的图像上滑动,现有以Q点为圆心,
的图像上滑动,现有以Q点为圆心,![]() 为半径的⊙Q,当⊙Q与直线
为半径的⊙Q,当⊙Q与直线![]() 相切时,求点Q的坐标.
相切时,求点Q的坐标.
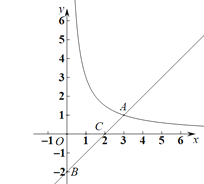
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com