
��ͼ1����֪��ABC�У�AB=10cm��AC=8cm��BC=6cm�������P��B������BA�����A�����˶���ͬʱ��Q��A������AC�������C�����˶������ǵ��ٶȾ�Ϊ2cm/s������PQ�����˶���ʱ��Ϊt����λ��s����0��t��4��������������⣺
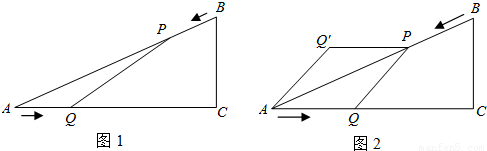
��1����tΪ��ֵʱ��PQ��BC��
��2�����AQP���ΪS����λ��cm2������S��t�ĺ�����ϵʽ
��3���Ƿ����ijʱ��t��ʹ�ı���BPQC�����Ϊ��ABC���������֮���������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��4����ͼ2���ѡ�AQP��AP���ۣ��õ��ı���AQPQ�䣮��ô�Ƿ����ijʱ��t��ʹ�ı���AQPQ��Ϊ���Σ�
��������
���������
��1����ʾ��AP��AQ��Ȼ��֡�AQP=90��͡�APQ=90��������������á�A��������ʽ���㼴�ɵý⣻
��2���������ABC�������Ȼ�����á�A�����������P��AQ�ľ��룬�ٸ��ݡ�APQ�������ʽ�г����̣�Ȼ����������б�ʽ����0��ȷ�������ڣ�
��3���������εĶԽ���ȣ��Խ���ƽ��һ��Խǿɵù���AB����ʱ����A=��APQ������Q��QD��AB��D�����ݵ������������ߺ�һ�����ʿɵ�AD=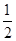 AP��Ȼ�����á�A��������ʽ���t��ֵ���ٸ����������DQ��Ȼ�����S����=2S��APQ���㼴�ɵý⣻����AC����ʱ����A=��AQP������P��PE��AC��E�����ݵ������������ߺ�һ�����ʿɵ�AE=
AP��Ȼ�����á�A��������ʽ���t��ֵ���ٸ����������DQ��Ȼ�����S����=2S��APQ���㼴�ɵý⣻����AC����ʱ����A=��AQP������P��PE��AC��E�����ݵ������������ߺ�һ�����ʿɵ�AE=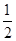 AQ��Ȼ�����á�A��������ʽ���t��ֵ���ٸ����������PE��Ȼ�����S����=2S��APQ���㼴�ɵý⣮
AQ��Ȼ�����á�A��������ʽ���t��ֵ���ٸ����������PE��Ȼ�����S����=2S��APQ���㼴�ɵý⣮
��4�����ȸ������ε����ʼ����������α����߶ι�ϵ�����PQ��QD��PD�ij��ȣ�Ȼ����Rt��PQD�У����ʱ��t��ֵ����������ε������ֵ��ע��������ε�������ڡ�AQP�����2�����Ӷ��������ã�2���С�AQP����ı���ʽ���������Ի�����㣮
���������
�⣺��AB=10cm��AC=8cm��BC=6cm��
���ɹ��ɶ����涨���á�ABCΪֱ�������Σ���CΪֱ�ǣ�
��1��BP=2t����AP=10��2t��
��PQ��BC��
��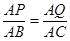 ����
����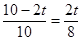 �����t=
�����t=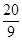 ��
��
�ߵ�t=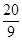 sʱ��PQ��BC��
sʱ��PQ��BC��
��2�����ͼ1��ʾ����P����PD��AC�ڵ�D��
��PD��BC����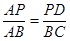 ����
����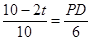 �����PD=6��
�����PD=6��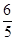 t��
t��
S=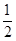 ��AQ��PD=
��AQ��PD=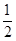 ��2t����6��
��2t����6��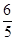 t��=��
t��=��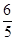 t2+6t=��
t2+6t=��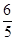 ��t��
��t��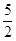 ��2+
��2+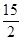 ��
��
�൱t=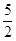 sʱ��Sȡ�����ֵ�����ֵΪ
sʱ��Sȡ�����ֵ�����ֵΪ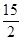 cm2��
cm2��
��3���������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
����S��AQP=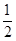 S��ABC����S��ABC=
S��ABC����S��ABC=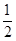 AC��BC=24�����ʱS��AQP=12��
AC��BC=24�����ʱS��AQP=12��
�ɣ�2����֪��S��AQP=��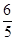 t2+6t��
t2+6t��
�ੁ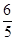 t2+6t=12������ã�t2��5t+10=0��
t2+6t=12������ã�t2��5t+10=0��
�ߡ�=����5��2��4��1��10=��15��0���˷����⣬
�����ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
��4���������ʱ��t��ʹ�ı���AQPQ��Ϊ���Σ�����AQ=PQ=BP=2t��
���ͼ2��ʾ����P����PD��AC�ڵ�D������PD��BC��
��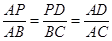 ����
����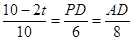 ��
��
��ã�PD=6��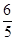 t��AD=8��
t��AD=8��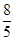 t��
t��
��QD=AD��AQ=8��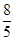 t��2t=8��
t��2t=8��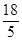 t��
t��
��Rt��PQD�У��ɹ��ɶ����ã�QD2+PD2=PQ2��
����8��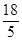 t��2+��6��
t��2+��6��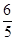 t��2=��2t��2��
t��2=��2t��2��
����ã�13t2��90t+125=0����ã�t1=5��t2=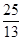 ��
��
��t=5sʱ��AQ=10cm��AC�����������⣬��ȥ����t=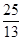 ��
��
���㣺 1.���κ����Ľ���ʽ�����κ�����Ӧ�ã�2.���κ��������ֵ����Сֵ��3.���ε����ʼ��ж�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ�
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ�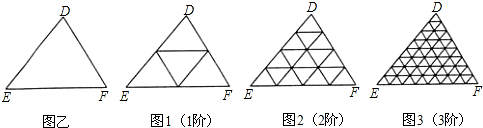
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ������֪��ABC�У�D��E�ֱ�ΪAB��AC���е㣬��ɵ�DE��BC����DE=
��ͼ������֪��ABC�У�D��E�ֱ�ΪAB��AC���е㣬��ɵ�DE��BC����DE=| 1 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com