练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标是（　　）
    A．（-4，0）B．（6，0）C．（-4，0）或（6，0）D．（0，12）或（0，-8）

    分析 根据B点的坐标可知AP边上的高为2，而△PAB的面积为5，点P在x轴上，说明AP=5，已知点A的坐标，可求P点坐标．

    解答 解：∵A（1，0），B（0，2），点P在x轴上，
    ∴AP边上的高为2，
    又△PAB的面积为5，
    ∴AP=5，
    而点P可能在点A（1，0）的左边或者右边，
    ∴P（-4，0）或（6，0）．
    故选C

    点评 本题考查了直角坐标系中，利用三角形的底和高及面积，表示点的坐标．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．-2015的相反数为（　　）
    A．-2015B．$\frac{1}{2015}$C．2015D．±2015

    查看答案和解析>>

    科目：初中数学 来源：2017届福建省仙游县郊尾、枫亭五校教研小片区九年级下学期第一次月考数学试卷（解析版） 题型：解答题

    某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：(注:获利=售价-进价)

    （1）若商店计划销售完这批商品后能获利1100元，问甲、乙两种商品应分别购进多少件?

    （2）若商店计划投入资金少于4290元，且销售完这批商品后获利多于1260元，请问共有几种购货方案?

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，在平行四边形ABCD中，点E是BC的中点，∠BOE=30°，OD=2，cos∠ADB=$\frac{{\sqrt{3}}}{2}$．则CD=$\frac{4\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．
    （1）按要求作图：
    ①画出△ABC关于原点O的中心对称图形△A1B1C1；
    ②画出将△ABC绕点O顺时针旋转90°得到△A2B2C2；
    （2）按照（1）中②作图，回答下列问题：△A2B2C2中顶点A2坐标为（4，2）；若P（a，b）为△ABC边上一点，则点P对应的点Q的坐标为（b，-a）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知AD∥BC，∠E=∠F，求证：∠B=∠D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．不等式组$\left\{\begin{array}{l}{x+1＞0}\\{x-2≤-1}\end{array}\right.$中的两个不等式的解集在同一个数轴上表示正确的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．【问题情境】
    张老师给爱好学习的小林和小兰提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

    小林的证明思路是：如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
    小兰的证明思路是：如图②，过点P作PG⊥CF，垂足为G，通过证明四边形PDFG是矩形，
    可得：PD=GF，PE=CG，则PD+PE=CF．
    【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD-PE=CF；
    【结论运用】请运用上述解答中所积累的经验和方法完成下列两题：
    如图④，在平面直角坐标系中有两条直线l1：y=$\frac{3}{4}$x+3、l2：y=-3x+3，若l2上的一点M到l1的距离是1，请运用上述的结论求出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

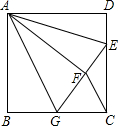    10．如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①点G是BC中点；②FG=FC；③S△FGC=$\frac{9}{10}$．其中正确的有①③（填写序号）．

    查看答案和解析>>

    同步练习册答案