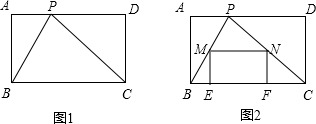
(1)证明:∵∠BPC=90°,∠D=90°,
∴∠BPA+∠DPC=∠PCD+∠DPC=90°,
∴∠APB=∠PCD;
又∵∠A=∠D=90°,
∴△ABP∽△DPC.
(2)解:设AP=x,则PD=AD-AP=13-x;
由(1)知:△ABP∽△DPC,得:
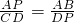
,即

,化简得:
x
2-13x+36=0,解得x=4,x=9;
在Rt△APB中,当AP=4时,tan∠APB=
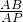
=

;
当AP=9时,tan∠APB=
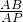
=
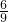
=

;
由于AD∥BC,则∠APB=∠PBC,
故∠PBC的正切值为

或

.
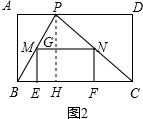
(3)解:过P作PH⊥BC于H,交MN于G,则PG⊥MN;
由题意知:AB=6,AD=AP+PD=12,即AD=2AB;
①当MN=2ME时,设ME=x,则MN=2x,PG=6-x;
由于MN∥BC,则△PMN∽△PBC,得:
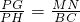
,即

;
解得:x=3,故MN=2x=6;
②当ME=2MN时,设MN=m,则ME=2m,PG=6-2m,同①可得:
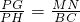
,即
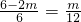
;
解得:m=2.4,即MN=2.4;
综上所述,MN的值为6或2.4.
分析:(1)若∠BPC=90°,则∠BPA和∠PCD同为∠DPC的余角,故∠BPA=∠PCD,而∠A、∠D都是直角,由此可证得:△ABP∽△DPC.
(2)由于AD∥BC,则∠PBC=∠APB,那么只需求出∠APB的正切值即可,关键是求AP的长;可设AP为x,用x可表示出DP的长,根据(1)所得相似三角形的比例线段,即可求得x即AP的值,进而可得到∠APB的正切值,由此得解.
(3)易得AB、AD的长,即可得到矩形的长和宽的比例关系,若设ME=x,则MN=2ME=2x,可过P作BC的垂线,设垂足为H,交MN于G;那么PG=6-x,易证得△PMN∽△PBC,根据相似三角形的对应边成比例,即可求得x的值,进而可求出MN的长.(当ME=2MN时,方法同上).
点评:此题重点考查的是相似三角形的判定和性质,涉及到的知识点有:矩形的性质、锐角三角函数等知识;本题难度虽然不大,但关键在于(2)(3)题都要把各种情况考虑到,以免漏解.


 (1)证明:∵∠BPC=90°,∠D=90°,
(1)证明:∵∠BPC=90°,∠D=90°,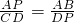 ,即
,即 ,化简得:
,化简得: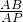 =
= ;
;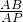 =
=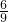 =
= ;
; 或
或 .
.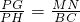 ,即
,即 ;
;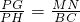 ,即
,即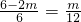 ;
;

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案