
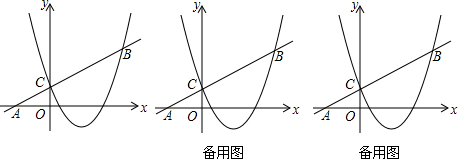
分析 (1)易得点C的坐标为(0,1),然后把点B、点C的坐标代入抛物线的解析式,即可解决问题;
(2)把B(4,3)代入y=kx+1中,即可得到k的值,从而可求出点A的坐标,就可求出tan∠CAO=$\frac{1}{2}$(即tan∠PAQ=$\frac{1}{2}$),设PQ=m,则QA=2m,根据条件tan∠NAQ-tan∠MPQ=$\frac{1}{2}$,即可求出PN的值;
(3)由条件CD⊥AB,CD=AC,想到构造全等三角形,过点D作DF⊥CO于点F,易证△ACO≌△CDF,从而可以求出FD、CF、OF.作PH∥CN,交y轴于点H,连接DH,易证四边形CHPN是平行四边形,从而可得CN=HP,CH=PN,通过计算可得DH=PN,从而可得△PHD是以PN、PD、NC的长为三边长的三角形,则有S△PHD=$\frac{25}{8}$.延长FD、PQ交于点G,易得∠G=90°.由点P在y=$\frac{1}{2}$x+1上,可设P(t,$\frac{1}{2}$t+1),根据S四边形HFGP=S△HFD+S△PHD+S△PDG,可求出t的值,从而得到点P、N的坐标及tan∠DPG的值,从而可得tan∠DPG=tan∠HDF,则有∠DPG=∠HDF,进而可证到∠HDP=90°.若△ENP与△PDH全等,已知PN=DH,可分以下两种情况(①∠ENP=∠PDH=90°,EN=PD,②∠NPE=∠HDP=90°,BE=PD)进行讨论,即可解决问题.
解答 解:(1)当x=0时,由y=kx+1得y=1,则C(0,1).
∵抛物线y=ax2-(6a-2)x+b(a≠0)经过C(0,1),B(4,3),
∴$\left\{\begin{array}{l}{b=1}\\{3=16a-4(6a-2)+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=1}\end{array}\right.$,
∴a=$\frac{3}{4}$;
(2)把B(4,3)代入y=kx+1中,得
3=4k+1,解得:k=$\frac{1}{2}$,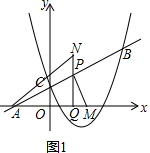
∴直线AB的解析式为y=$\frac{1}{2}$x+1.
由y=0得0=$\frac{1}{2}$x+1,
解得:x=-2,
∴A(-2,0),OA=2,
∵C(0,1),
∴OC=1,
∴tan∠CAO=$\frac{OC}{OA}$=$\frac{1}{2}$.
∵PQ⊥x轴,
∴tan∠PAQ=$\frac{PQ}{QA}$=$\frac{1}{2}$,
设PQ=m,则QA=2m,
∵tan∠NAQ-tan∠MPQ=$\frac{1}{2}$,
∴$\frac{NQ}{QA}-\frac{MQ}{PQ}$=$\frac{1}{2}$,
∵MQ=$\frac{5}{8}$,
∴$\frac{PN+m}{2m}$-$\frac{\frac{5}{8}}{m}$=$\frac{1}{2}$,
∴PN=$\frac{5}{4}$;
(3)方法一:
在y轴左侧抛物线上存在E,使得△ENP与以PN,PD,NC的长为三边长的三角形全等.
过点D作DF⊥CO于点F,如图2,
∵DF⊥CF,CD⊥AB,
∴∠CDF+∠DCF=90°,∠DCF+∠ACO=90°,
∴∠CDF=∠ACO,
∵CO⊥x轴,DF⊥CO,
∴∠AOC=∠CFD=90°,
在△ACO和△CDF中,
$\left\{\begin{array}{l}{∠ACO=∠CDF}\\{∠AOC=∠CFD}\\{CA=CD}\end{array}\right.$,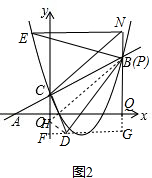
∴△ACO≌△CDF(AAS),
∴CF=AO=2,DF=CO=1,
∴OF=CF-CO=1,
作PH∥CN,交y轴于点H,连接DH,
∵CH∥PN,
∴四边形CHPN是平行四边形,
∴CN=HP,CH=PN=$\frac{5}{4}$,
∴HF=CF-CH=$\frac{3}{4}$,DH=$\sqrt{D{F}^{2}+H{F}^{2}}$=$\frac{5}{4}$,
∴DH=PN.
∴△PHD是以PN,PD,NC的长为三边长的三角形,
∴S△PHD=$\frac{25}{8}$.
延长FD、PQ交于点G,
∵PQ∥y轴,
∴∠G=180°-∠CFD=90°,
∴S四边形HFGP=S△HFD+S△PHD+S△PDG,
∴$\frac{1}{2}$(HF+PG)FG=$\frac{1}{2}$HF•FD+$\frac{25}{8}$+$\frac{1}{2}$DG•PG.
∵点P在y=$\frac{1}{2}$x+1上,∴可设P(t,$\frac{1}{2}$t+1),
∴$\frac{1}{2}$($\frac{3}{4}$+$\frac{1}{2}$t+1+1)•t=$\frac{1}{2}$×$\frac{3}{4}$×1+$\frac{25}{8}$+$\frac{1}{2}$(t-1)•($\frac{1}{2}$t+1+1),
∴t=4,P(4,3),
∴N(4,$\frac{17}{4}$),tan∠DPG=$\frac{DG}{PG}$=$\frac{3}{4}$.
∵tan∠HDF=$\frac{HF}{FD}$=$\frac{3}{4}$,
∴∠DPG=∠HDF.
∵∠DPG+∠PDG=90°,
∴∠HDF+∠PDG=90°,
∴∠HDP=90°.
∵PN=DH,若△ENP与△PDH全等,则有两种情况:
①当∠ENP=∠PDH=90°,EN=PD时,
∵PD=$\sqrt{P{G}^{2}+D{G}^{2}}$=5,∴EN=5,
∴E(-1,$\frac{17}{4}$).
由(1)得:抛物线y=$\frac{3}{4}$x2-$\frac{5}{2}$x+1.
当x=-1时,y=$\frac{17}{4}$,所以点E在此抛物线上.
②当∠NPE=∠HDP=90°,BE=PD时,
则有E(-1,3),此时点E不在抛物线上,
∴存在点E,满足题中条件,点E的坐标为(-1,$\frac{17}{4}$).
方法二:
作BF∥CN交y轴于点F,如图3,
∴NC=PF,PN=CF=$\frac{5}{4}$,F(0,-$\frac{1}{4}$),
∵CD⊥AB,且CD=AC,
∴点D可视为点A绕点C逆时针旋转90°而成,将点C(0,1)平移至原点C′(0,0),则点A′(-2,-1),
将点A′绕原点逆时针旋转90°,则D′(1,-2),将C′(0,0)平移至点C(0,1),
则D′平移后即为点D(1,-1),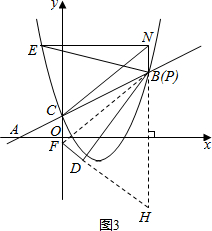
∴lDF:y=-$\frac{3}{4}$x-$\frac{1}{4}$,
过点P作x轴垂线交FD的延长线于H,
∵P(t,$\frac{1}{2}$t+1),∴H(t,-$\frac{3}{4}$t-$\frac{1}{4}$),
∴S△PDF=$\frac{1}{2}({P}_{Y}-{H}_{Y})({D}_{X}-{F}_{X})=\frac{25}{8}$,
∴$\frac{1}{2}×(\frac{1}{2}t+1+\frac{3}{4}t+\frac{1}{4})(1-0)=\frac{25}{8}$,
∴t=4,∴P(4,3),D(1,-1),F(0,-$\frac{1}{4}$),
∴PD2=25,PN2=$\frac{25}{16}$,
∴PD2+PN2=$\frac{425}{16}$,PF2=42+(3+$\frac{1}{4}$)2=$\frac{425}{16}$,
∴PD2+PN2=PF2,
∴以PN,PD,NC的长为三边长的三角形为直角三角形,欲使△ENP全等于上述三角形,则必有直角
①过点P作PE⊥PN交抛物线于点E,∴E(-$\frac{2}{3}$,3)(舍)
②过点N作PE⊥PN交抛物线于点E,∴E(-1,$\frac{17}{4}$).
点评 本题主要考查了运用待定系数法求直线及二次函数的解析式、全等三角形的判定与性质、平行四边形的判定与性质、三角函数的定义、抛物线上点的坐标特征、勾股定理等知识,通过平移CN,将PN、PD、NC归结到△PHD中,是解决本题的关键.在解决问题的过程中,用到了分类讨论、平移变换、割补法、运算推理等重要的数学思想方法,应学会使用.


科目:初中数学 来源: 题型:填空题
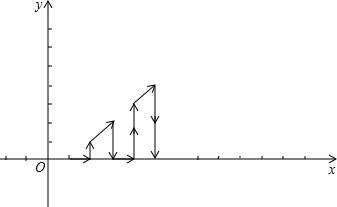 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
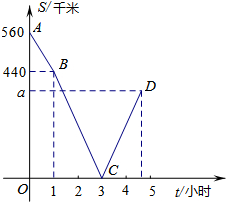 甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )
甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com