
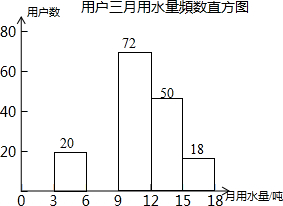
 每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
每年5月的第二周为我国城市节约用水宣传周.某社区为了做好今年居民节约用水的宣传,从本社区6000户家庭中随机抽取200户,调查他们家庭今年三月份的用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用水量h(吨) | 频数 | 频率 |
| h≤3 | 0 | 0 |
| 3<h≤6 | 20 | 0.10 |
| 6<h≤9 | m | 0.20 |
| 9<h≤12 | 72 | 0.36 |
| 12<h≤15 | 50 | n |
| 15<h≤18 | 18 | 0.09 |
| 18<h | 0 | 0 |
分析 (1)根据直方图和从本社区6000户家庭中随机抽取200户,可以得到m的值,由表格中的频率n对应的频数50可以求得相应的频率;
(2)根据第一问求得的m值,可以将直方图补充完整;
(3)根据200户的用水量可以估算出这个小区6000户超过12吨的住户.
解答  解:(1)由题意和直方图可得,
解:(1)由题意和直方图可得,
6<h≤9的用户是:m=200-20-70-50-18=40,
由表格可得,n=50÷200=0.25,
故答案为:40,0.25;
(2)补全频数直方图如右图所示,
(3)由题意和表格,可得
6 000×(0.25+0.09)=2040(户)
答:该社区约有2040户家庭三月份的用水量超过基本月用水量.
点评 本题考查频数分布直方图、用样本估计总体、频数分布表,解题的关键是明确题意,找出所求问题需要的条件,会用样本估计总体.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 99.55×102 | B. | 9.955×103 | C. | 9.9×103 | D. | 10×103 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A.与x轴、y轴分别交于点B、C,过点A作AD⊥x轴于点D,过点D作DE∥AB,交y轴于点E.己知四边形ADEC的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )
如图,边长分别为1和2的两个等边三角形,开始它们在左边重叠,大△ABC固定不动,然后把小△A′B′C′自左向右平移,直至移到点B′到C重合时停止.设小三角形移动的距离为x,两个三角形的重合部分的面积为y,则y关于x的函数图象是( )| A. |  | B. |  | C. |  | D. | 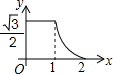 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.
如图,在△ABC中,∠BAC=90°,AB=8,AC=6,O为BC的中点,OE平分∠AOB,与AB相交于点E,OD平分∠AOC,与AC相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
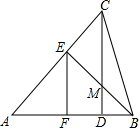 在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.
在△ABC中,CD是高,在边AC上有一点E,使EA=EB连接EB交CD于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com