
【题目】如图,把两个全等的矩形![]() 和矩形
和矩形![]() 拼成如图所示的图案,连接
拼成如图所示的图案,连接![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转,点
逆时针旋转,点![]() 的运动轨迹交
的运动轨迹交![]() 于点
于点![]() ,若
,若![]() ,有以下四个结论:①
,有以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④阴影部分的面积为
;④阴影部分的面积为![]() .其中一定成立的是______.(把所有正确结论的序号填在横线上)
.其中一定成立的是______.(把所有正确结论的序号填在横线上)
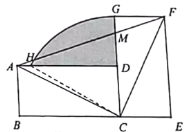
【答案】①③④
【解析】
根据四边形ABCD,EFGC为全等的矩形,得到AB=CE,∠B=∠E=90°,BC=EF,即可得到△ABC≌△CEF,根据全等的性质得到∠ACB=∠CFE,AC=CF,可得![]() 同理可证△ABC≌△FGC (SAS) ,可判别②错误,利用平行线段成比例可得
同理可证△ABC≌△FGC (SAS) ,可判别②错误,利用平行线段成比例可得![]() ,可求出MD的长,即可得出
,可求出MD的长,即可得出![]() ,进行判断③
,进行判断③
;利用![]() 可计算出阴影部分面积,进行判断④
可计算出阴影部分面积,进行判断④
证明: (1)∵四边形ABCD,EFGC为全等的矩形,
∴AB= CE,∠B=∠E= 90°BC= EF
在△ABC和△CEF中,
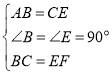
∴△ABC≌△CEF(SAS) ,
∴∠ACB=∠CFE,AC= CF
∴![]()
故①正确,
∵四边形ABCD,EF GC为全等的矩形,
∴AB= GF,∠B=∠CGF= 90°BC= CG
在△ABC和△FGC中,
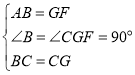
∴△ABC≌△FGC (SAS) ,
故②错误,
∵GF//AD
∴![]()
∵CG=4,CD=2
∴GD=2
∴![]()
在Rt△ADM中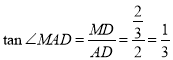
故③正确;
∵四边形ABCD是矩形,
∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CH=BC=4,CH=2CD.
∴∠DHC=30°,
∴∠DCH=60°.
由勾股定理得DE=![]()
∴![]()
故④正确
故答案为:①③④


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】如图①,在四边形![]() 中,
中,![]() 于点
于点![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() 为线段
为线段![]() 上的点,且
上的点,且![]() .
.
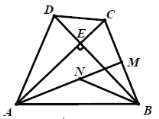
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,连接
,连接![]() ,当四边形
,当四边形![]() 为平行四边形时,求线段
为平行四边形时,求线段![]() 的长;
的长;
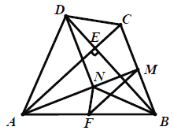
(3)若点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() (如图②),求证:
(如图②),求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与反比例函数![]() 的图象交于点A已知点
的图象交于点A已知点![]() ,点C是反比例函数
,点C是反比例函数![]() 的图象上的一个动点过点C作x轴的垂线,交直线AB于点D.
的图象上的一个动点过点C作x轴的垂线,交直线AB于点D.

(1)求k的值.
(2)若![]() ,求
,求![]() 的面积.
的面积.
(3)在点C运动的过程中,是否存在点C,使![]() ?若存在,请求出点C的坐标;若不存在,请说明理由.
?若存在,请求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站 | A | B | C | D | E |
x(千米) | 8 | 9 | 10 | 11.5 | 13 |
y1(分钟) | 18 | 20 | 22 | 25 | 28 |
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=![]() x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知点
,已知点![]() 为抛物线第一象限上一动点,连接
为抛物线第一象限上一动点,连接![]() 、
、![]() 、
、![]() .
.
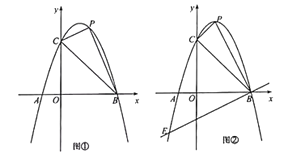
(1)求抛物线的解析式,并直接写出抛物线的顶点坐标;
(2)当![]() 的面积最大时,求出点
的面积最大时,求出点![]() 的坐标;
的坐标;
(3)如图②,当点![]() 与抛物线顶点重合时,过点
与抛物线顶点重合时,过点![]() 的直线
的直线![]() 与抛物线交于点
与抛物线交于点![]() ,在直线
,在直线![]() 上方的抛物线上是否存在一点
上方的抛物线上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条边AB=1,AD=![]() ,以B为旋转中心,将对角线BD顺时针旋转60°得到线段BE,再以C为圆心将线段CD顺时针旋转90°得到线段CF,连接EF,则图中阴影部分面积为_____.
,以B为旋转中心,将对角线BD顺时针旋转60°得到线段BE,再以C为圆心将线段CD顺时针旋转90°得到线段CF,连接EF,则图中阴影部分面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
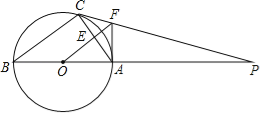
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
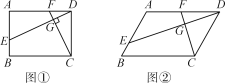
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:![]() ;
;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论.
成立?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com