
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 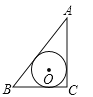 B.
B. 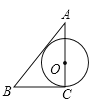
C. 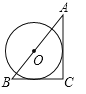 D.
D. 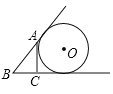
【答案】C
【解析】
A.由三角形的内切圆的性质,即可求得⊙O的半径;
B.易证得△ADO∽△ACB,然后由相似三角形的对应边成比例,即可求得⊙O的半径;
C.易证得四边形ODCE是正方形,然后由平行线分线段成比例定理,求得⊙O的半径;
D.易证得四边形ODCE是正方形,利用切线长定理,由勾股定理即可求得⊙O的半径.
设⊙O的半径为r. A.
∵⊙O是△ABC内切圆,∴S△ABC![]() (a+b+c)r
(a+b+c)r![]() ab,∴r
ab,∴r![]() ;
;
B.如图,连接OD,则OD=OC=r,OA=b﹣r.
∵AD是⊙O的切线,∴OD⊥AB,即∠AOD=∠C=90°,∴△ADO∽△ACB,∴OA:AB=OD:BC,即(b﹣r):c=r:a,解得:r![]() ;
;
C.连接OE,OD.
∵AC与BC是⊙O的切线,∴OE⊥BC,OD⊥AC,∴∠OEB=∠ODC=∠C=90°,∴四边形ODCE是矩形.
∵OD=OE,∴矩形ODCE是正方形,∴EC=OD=r,OE∥AC,∴OE:AC=BE:BC,∴r:b=(a﹣r):a,∴r![]() ;
;
D.设AC、BA、BC与⊙O的切点分别为D、F、E,连接OD、OE.
∵AC、BE是⊙O的切线,∴∠ODC=∠OEC=∠DCE=90°,∴四边形ODCE是矩形.
∵OD=OE,∴矩形ODCE是正方形,即OE=OD=CD=r,则AD=AF=b﹣r.
连接OB,OF,由勾股定理得:BF2=OB2﹣OF2,BE2=OB2﹣OE2.
∵OB=OB,OF=OE,∴BF=BE,则BA+AF=BC+CE,c+b﹣r=a+r,即r![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】不能构成三角形的三条整数长度的线段的长度和的最小值为1+1+2=4;若四条整数长度的线段中,任意三条不能构成三角形,则该四条线段的长度和的最小值为1+1+2+3=7;……,依此规律,若八条整数长度的线段中,任意三条不能构成三角形,则该八条线段的长度和的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
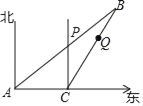
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿某一方向直航140海里的海岛B,其速度为14海里/小时;乙船速度为20海里/小时,先沿正东方向航行3小时后,到达C港口接旅客,停留1小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(1)求海岛B到航线AC的距离;
(2)甲船在航行至P处,发现乙船在其正东方向的Q处,问此时两船相距多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 | 甲 | 乙 | 丙 | 丁 |
放出风筝线长 | 140m | 100m | 95m | 90m |
线与地面夹角 | 30° | 45° | 45° | 60° |
A、甲B、乙
C、丙D、丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=2BC,在直线BC或AC上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )

A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com