
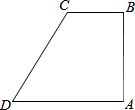
 如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为2或2$\sqrt{3}$或4.
如图,在四边形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P为四边形ABCD边上的任意一点,当∠BPC=30°时,CP的长为2或2$\sqrt{3}$或4. 分析 如图,连接AC.首先证明△ACD是等边三角形,分三种情形讨论即可解决问题.
解答 解:如图,连接AC.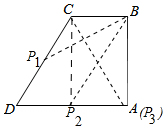
∵BC∥AD,∠DCB=120°,
∴∠D+∠DCB=180°,
∴∠D=60°,
∵DC=DA,
∴△ACD是等边三角形,
∴∠DAC=60°,
∵AB⊥BC,
∴∠CBA=∠BAD=90°,
∴∠BAC=30°,
∴当P3与A重合时,∠BP3C=30°,此时CP3=4,
作CP2⊥AD于P2,则四边形BCP2A是矩形,
易知∠CP2B=30°,此时CP2=2$\sqrt{3}$,
当CB=CP1时,∠CP1B=∠CBP1=30°,此时CP1=2,
综上所述,CP的长为2或2$\sqrt{3}$或4.
故答案为2或2$\sqrt{3}$或4.
点评 本题考查等边三角形的判定、矩形的判定、30度的直角三角形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
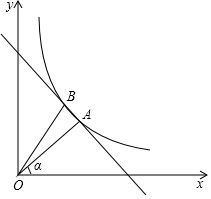 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
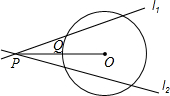 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )| A. | 0°<α<30° | B. | 0°<α<45° | C. | 0°<α<60° | D. | 0°<α<90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
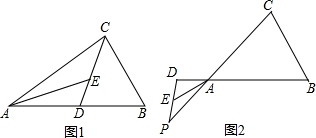
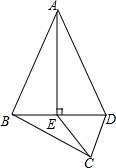 如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )
如图,四边形ABCD中,AB=AD,AE⊥BD于点E,连接CE.如果AB=13,BC=2$\sqrt{21}$,CD=4,AE=12,那么CE的长度是( )| A. | 5 | B. | 8 | C. | 10 | D. | 无法计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种货车辆数(单位:辆) | 2 | 5 |
| 乙种货车辆数(单位:辆) | 3 | 6 |
| 累计货运吨数(单位:吨) | 15.5 | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com