
 如图,⊙O的直径AB长为6,点C、E是圆上一点,且∠AEC=30°.过点C作CD⊥AB,垂足为点D,则AD的长为$\frac{3}{2}$.
如图,⊙O的直径AB长为6,点C、E是圆上一点,且∠AEC=30°.过点C作CD⊥AB,垂足为点D,则AD的长为$\frac{3}{2}$. 科目:初中数学 来源: 题型:解答题
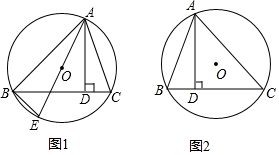 学习了“直径所对的圆周角是直角”这一性质后,圆中借助直角转化的等角较为灵活方便,比如说:
学习了“直径所对的圆周角是直角”这一性质后,圆中借助直角转化的等角较为灵活方便,比如说:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 带“+”号的数是正数,带“-”号的数是负数 | |
| B. | 因为+0=-0=0,所以零既是正数,又是负数 | |
| C. | 3.14-π是负数 | |
| D. | -x是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
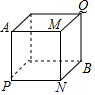 如图,一只蚂蚁沿边长为a的正方体表面从点A爬到点B,则它走过的路程最短为( )
如图,一只蚂蚁沿边长为a的正方体表面从点A爬到点B,则它走过的路程最短为( )| A. | $\sqrt{3}$a | B. | (1+$\sqrt{2}$)a | C. | 3a | D. | $\sqrt{5}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
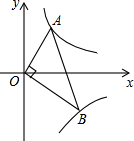 如图,已知点A,B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{-8}{x}$(x>0)的图象上且OA⊥OB,则OA:OB为( )
如图,已知点A,B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{-8}{x}$(x>0)的图象上且OA⊥OB,则OA:OB为( )| A. | $\frac{1}{\sqrt{2}}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{\sqrt{3}}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com