
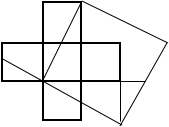
 如图是五个全等的小正方形,请剪二刀,把它拼成一个正方形,并画出所拼的正方形.
如图是五个全等的小正方形,请剪二刀,把它拼成一个正方形,并画出所拼的正方形. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:
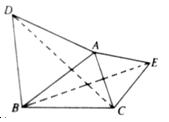
如图, ![]() 和
和![]() 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.

1.(1)请判断:线段BE与CD的大小关系是 ;
2.(2)观察图,当![]() 和
和![]() 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
3.(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是 ,在图4中证明你的猜想.

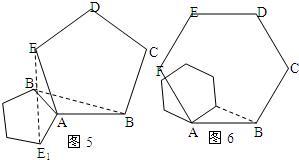
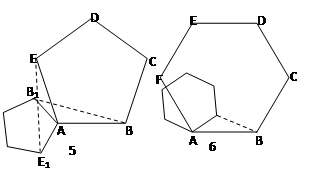
4.(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?
查看答案和解析>>
科目:初中数学 来源:2011-2012年福建省初三第一学期第一次月考数学卷 题型:解答题
如图,  和
和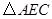 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.

1.(1)请判断:线段BE与CD的大小关系是 ;
2.(2)观察图,当 和
和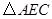 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
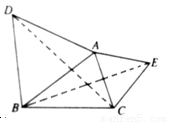
3.(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是 ,在图4中证明你的猜想.

4.(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是 ;它们分别在哪两个全等三角形中 ;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com