

分析 (1)根据条形统计图和扇形统计图可知A有90人占调查总数的30%,从而可以求出被调查的居民数;
(2)根据条形统计图和扇形统计图可知A有90人占调查总数的30%,可以求得选B和选C的人数以及B、D所占的百分比,从而可以将统计图补充完整;
(3)由C所占的百分比可以求得图2中“C”层次所在扇形的圆心角的度数;
(4)根据条形统计图和扇形统计图,估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
解答 解:(1)由条形统计图和扇形统计图可知A有90人占调查总数的30%,
∴本次被抽查的居民有:90÷30%=300(人),
即本次被抽查的居民有300人;
(2)由条形统计图和扇形统计图可得,
选C的人数有:300×20%=60人,
选B的人数有:300-90-60-30=120(人),
B所占的百分比为:120÷300=40%,
D所占的百分比为:30÷300=10%,
∴补全的图1和图2如右图所示,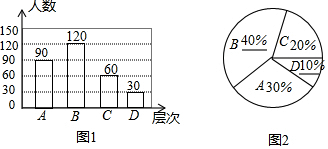
(3)由题意可得,
图2中“C”层次所在扇形的圆心角的度数是:360°×20%=72°,
即图2中“C”层次所在扇形的圆心角的度数是72°;
(4)由题意可得,4000×(30%+40%)=2800(人),
答:该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.
点评 本题考查条形统计图、扇形统计图、用样本估计总体,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
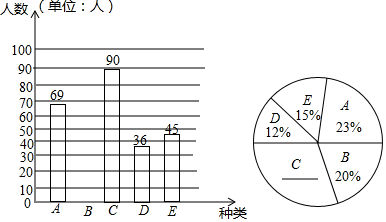
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
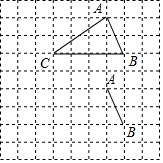 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②④ | B. | ①③ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券 | 10 | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com