
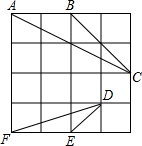
 在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.分析 (1)利用图形结合正方形的性质以及三角形面积公式得出即可;
(2)利用相似三角形的判定方法得出即可;
(3)将三角形的三边变为原来的$\frac{1}{2}$,进而得出答案.
解答 解:(1)由题意可得:∠ABC=90°+45°=135°,
△ABC的面积为=$\frac{1}{2}$×2×2=2;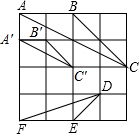 (2)相似,
(2)相似,
理由:∵AB=2BC=2$\sqrt{2}$,AC=2$\sqrt{5}$,DE=$\sqrt{2}$,EF=2,DF=$\sqrt{10}$,
∴$\frac{AB}{DE}$=$\frac{BC}{EF}$=$\frac{AC}{DF}$=$\sqrt{2}$,
∴△ABC∽△DEF;
(3)如图所示:△A′B′C′.
故答案为:135,2.
点评 此题主要考查了作图-相似变换,相似三角形的判定与性质,正确结合网格求出答案是解题关键.


科目:初中数学 来源: 题型:填空题
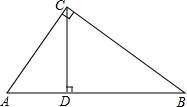 如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)
如图,△ABC为直角三角形,∠ACB=90°,CD为斜边AB上的高,D为垂足,△ABC∽△ACD∽△CBD,那么下列等式:①AC2=AD•AB;②CD2=AD•BD;③BC2=BD•AB;④AC•CB=BA•CD,其中正确的有①②③④.(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
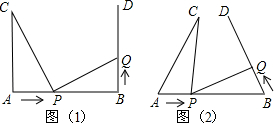
 如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).
如图,在矩形ABCD中,AB=4,AD=2.点P,Q同时从点A出发,点P以每秒2个单位的速度沿A→B→C→D的方向运动;点Q以每秒1个单位的速度沿A→D→C的方向运动,当P,Q两点相遇时,它们同时停止运动.设P,Q两点运动的时间为x(秒),△APQ的面积为S(平方单位).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com