
【题目】汽车公司有甲、乙两种货车可供租用,现有一批货物要运往某地,货主准备租用该公司货车,已知以往甲、乙两种货车运货情况如下表:

(1)甲、乙两种货车每辆可装多少吨货物?
(2)若货主需要租用该公司的甲种货车8辆,乙种货车6辆,刚好运完这批货物,如按每吨付运费50元,则货主应付运费总额为多少元?
(3)若货主共有20吨货,计划租用该公司的货车正好(每辆车都满载)把这批货运完,该汽车公司共有哪几种运货方案?
【答案】(1)甲种货车每辆可装2吨货物,乙种货车每辆可装3吨货物;(2)货主应付运费总额为1700元;(3)该汽车公司可以租甲种货车10辆或甲种货车7辆、乙种货车2辆或甲种货车4辆、乙种货车4辆或甲种货车1辆、乙种货车6辆.
【解析】
(1)设甲种货车每辆可装x吨货物,乙种货车每辆可装y吨货物,根据题意,列出二元一次方程组,然后解方程组即可;
(2)先求出这批货物共有多少吨,然后乘每吨的运费即可;
(3)设租用该公司的甲种货车a辆,乙种货车b辆,根据题意,列出二元一次方程,然后求出所有的自然数解即可.
解:(1)设甲种货车每辆可装x吨货物,乙种货车每辆可装y吨货物
根据题意可得:![]()
解得:![]()
答:甲种货车每辆可装2吨货物,乙种货车每辆可装3吨货物.
(2)这批货物共有8×2+6×3=34(吨)
货主应付运费总额为34×50=1700(元)
答:货主应付运费总额为1700元.
(3)设租用该公司的甲种货车a辆,乙种货车b辆,
根据题意可得:2a+3b=20,
满足此二元一次方程的自然数解有:![]() 或
或![]() 或
或![]() 或
或![]()
答:该汽车公司可以租甲种货车10辆或甲种货车7辆、乙种货车2辆或甲种货车4辆、乙种货车4辆或甲种货车1辆、乙种货车6辆.


科目:初中数学 来源: 题型:
【题目】为鼓励居民节约用电,国家发改委发布文件在全国实行“阶梯电价”收费,重庆结合本市实际,根据国家发改委文件要求,决定从2016年1月1日起对居民生活用电实行“阶梯电价”收费,具体收费标准见下表.若2016年8月份,该市居民甲生活用电240千瓦时(能量量度单位,1千瓦时即1度),交电费130元.
一户居民一个月用电量 | 电费价格(元/千瓦时) | |
第一档 | 不超过200千瓦时 | 0.52 |
第二档 | 超过200千瓦时但不超过320千瓦时 |
|
第三档 | 超过320千瓦时 | 0.95 |
(1)求上表中的![]() 的值;
的值;
(2)若该市居民乙某月交电费220元,居民乙当月的生活用电量为多少千瓦时?
(3)实行“阶梯电价”收费后,该市居民丙月用电量为多少千瓦时,其当月的平均电价为0.55元/千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生的体育成绩,从全年级学生中随机抽取部分学生进行“双飞”跳绳测试,结果分为A,B,C,D四个等级,请跟进两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该学校七年级共有400名学生,请你估计该学校七年级学生中“双飞”跳绳测试结果为D等级的学生有多少名.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下面四个命题,其中真命题的个数有( )
(1)平分弦的直径垂直于这条弦,并且平分这条弦所对的弧;
(2)90°的圆周角所对的弦是直径;
(3)在同圆或等圆中,圆心角的度数是圆周角的度数的两倍;
(4)如下图,顺次连接圆的任意两条直径的端点,所得的四边形一定是矩形.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )

A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=3
,AH=3![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
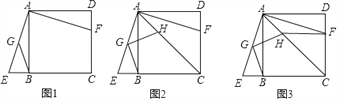
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com