
【题目】如图,已知O为直线AD上一点,OB是∠AOC内部一条射线且满足∠AOB与∠AOC互补,OM,ON分别为∠AOC,∠AOB的平分线.

(1)∠COD与∠AOB相等吗?请说明理由;
(2)若∠AOB=30°,试求∠AOM与∠MON的度数;
(3)若∠MON=42°,试求∠AOC的度数.
【答案】(1)相等,理由见解析;(2)∠AOM=75°,∠MON=60°;(3)132°
【解析】
(1)由题意可得∠AOC+∠AOB=180°,∠AOC+∠DOC=180°,可以根据同角的补角相等得到∠COD=∠AOB;
(2)根据互补的定义可求∠AOC,再根据角平分线的定义可求∠AOM,根据角平分线的定义可求∠AON,根据角的和差关系可求∠MON的度数;
(3)设∠AOB=x°,则∠AOC=180°-x°,列方程![]() ,解方程即可求解.
,解方程即可求解.
(1)∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)∵∠AOB与∠AOC互补,∠AOB=30°,
∴∠AOC=180°-30°=150°,
∵OM为∠AOB的平分线,
∴∠AOM=75°,
∵ON为∠AOB的平分线,
∴∠AON=15°,
∴∠MON=75°-15°=60°;
(3)设∠AOB=x°,则∠AOC=180°-x°.
由题意,得![]()
∴180-x-x=84,
∴-2x=-96,
解得x=48,
故∠AOC=180°-48°=132°.


科目:初中数学 来源: 题型:
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召,我市某街道决定从备选的五种树中选购一种进行栽种.为了更好地了解社情民意,工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:

请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为: ;
(2)请将条形统计图补充完整;
(3)请计算扇形统计图中“枫树”所在扇形的圆心角度数;
(4)已知该街道辖区内现有居民8万人,请你估计这8万人中最喜欢玉兰树的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(5分)某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):

⑴根据记录可知前三天共生产________辆;
⑵产量最多的一天比产量最少的一天多生产________辆;
⑶该厂实行计件工资制,每辆车60元,超额完成任务每辆奖15元,少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
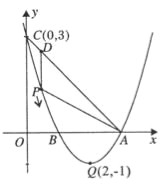
【题目】如图,已知抛物线![]() 的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
【1】求该抛物线的函数关系式;
【1】求点P在运动的过程中,线段PD的最大值;
【1】当△ADP是直角三角形时,求点P的坐标;
【1】在题(3)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
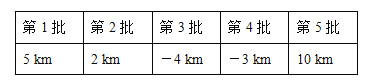
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对数轴上的点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点
表示的数乘以3,再把所得数对应的点向左平移1个单位,得到点![]() 的对应点
的对应点![]() .比如,点
.比如,点![]() 表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点
表示3,3乘以3得9,表示9的点向左平移1个单位为8,因此点![]() 的对应点
的对应点![]() 表示的数为8.
表示的数为8.
⑴点![]() ,
,![]() 在数轴上,对线段
在数轴上,对线段![]() 上的每个点进行上述操作后得到线段
上的每个点进行上述操作后得到线段![]() ,其中点
,其中点![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() .如图,若点
.如图,若点![]() 表示的数是1,则点
表示的数是1,则点![]() 表示的数是__________;若点
表示的数是__________;若点![]() 表示的数是
表示的数是![]() ,则点
,则点![]() 表示的数是__________.
表示的数是__________.
⑵若数轴上的点![]() 经过上述操作后,位置不变,则点
经过上述操作后,位置不变,则点![]() 表示的数是__________.
表示的数是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a-20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com