
 ,则BN的长是 ,
,则BN的长是 , 的值等于 ;若
的值等于 ;若 (
( ,且
,且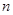 为整数),则
为整数),则 的值等于 (用含
的值等于 (用含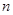 的式子表示).
的式子表示).
 ,
,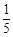 ,
,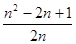
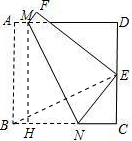
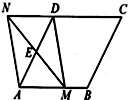
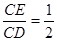 可得CE=DE=1,设BN=x,则NE=x,NC=2-x,在Rt△CNE中,根据勾股定理即可列方程求得x的值,从而得到BN的长,在Rt△ABM和在Rt△DEM中,根据勾股定理可得AM2+AB2=BM2,DM2+DE2=EM2,则AM2+AB2=DM2+DE2.设AM=y,则DM=2-y,
可得CE=DE=1,设BN=x,则NE=x,NC=2-x,在Rt△CNE中,根据勾股定理即可列方程求得x的值,从而得到BN的长,在Rt△ABM和在Rt△DEM中,根据勾股定理可得AM2+AB2=BM2,DM2+DE2=EM2,则AM2+AB2=DM2+DE2.设AM=y,则DM=2-y,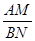 的值;当四边形ABCD为正方形时,连接BE,
的值;当四边形ABCD为正方形时,连接BE, ,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=
,不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,EN2=NC2+CE2,x2=(n-x)2+12,x=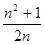 ;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,则NH=EC=1,AM=BH=BN-NH=
;作MH⊥BC于H,则MH=BC,又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;而∠NMH+∠BNM=90°,故∠EBC=∠NMH,则△EBC≌△NMH,则NH=EC=1,AM=BH=BN-NH=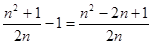 ,从而可以求得结果.
,从而可以求得结果.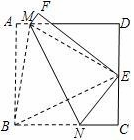
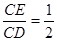 ,
,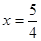 ,即
,即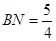
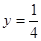 ,即
,即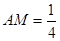
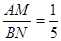
 ,
,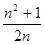 ;
;
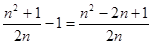
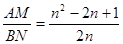 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B.2 | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
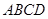 中,
中,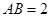 ,
,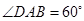 ,点
,点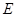 是
是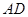 边的中点,点
边的中点,点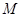 是
是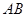 边上一动点(不与点
边上一动点(不与点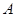 重合),延长
重合),延长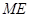 交射线
交射线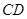 于点
于点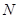 ,连接
,连接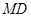 ,
,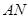 .
.
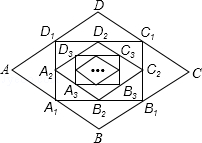
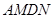 是平行四边形;
是平行四边形;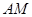 的值为 时,四边形
的值为 时,四边形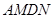 是矩形;
是矩形;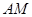 的值为 时,四边形
的值为 时,四边形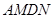 是菱形.
是菱形.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,DB="4," 求四边形ABCD的面积.
,DB="4," 求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.2a2 | B.3a2 | C.4a2 | D.5a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com