
【题目】如图,已知反比例函数![]() 的图象与直线
的图象与直线![]() 相交于点
相交于点![]() ,
,![]() .
.
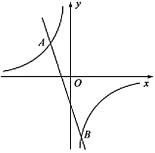
(1)求出直线![]() 的表达式;
的表达式;
(2)在![]() 轴上有一点
轴上有一点![]() 使得
使得![]() 的面积为18,求出点
的面积为18,求出点![]() 的坐标.
的坐标.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
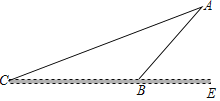
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图,已知原阶梯式自动扶梯AB的长为6![]() m,坡角∠ABE=45°,改造后的斜坡自动扶梯坡角∠ACB=15°,求改造后的斜坡式自动扶梯AC的长,(精确到0.1m,参考数据;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27)
m,坡角∠ABE=45°,改造后的斜坡自动扶梯坡角∠ACB=15°,求改造后的斜坡式自动扶梯AC的长,(精确到0.1m,参考数据;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AB=![]() .点D,E分别在边AB,AC上,将线段ED绕点E按逆时针方向旋转90°得到EF,连结BF,BF的中点为G.
.点D,E分别在边AB,AC上,将线段ED绕点E按逆时针方向旋转90°得到EF,连结BF,BF的中点为G.
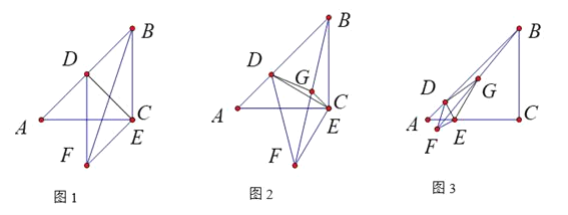
(1)当点E与点C重合时.
①如图1,若AD=BD,求BF的长.
②当点D从点A运动到点B时,求点G的运动路径长.
(2)当AE=3,点G在△DEF一边所在直线上时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法,“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图、左视图、俯视图依次是( )

A.(2)、(4)、(1)B.(3)、(1)、(2)
C.(1)、(4)、(2)D.(3)、(4)、(1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,判断△GEF的形状,并说明理由;
(3)如图3,若AB=![]() ,过点M作MG⊥EF交线段BC的延长线于点G.
,过点M作MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
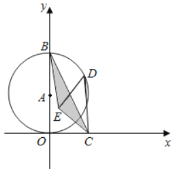
【题目】如图,在平面直角坐标系中,以点A(0,2)为圆心,2为半径的圆交y轴于点B.已知点C(2,0),点D为⊙A上的一动点,以CD为斜边,在CD左侧作等腰直角三角形CDE,连结BC,则△BCE面积的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角等腰三角形ABC中,AB=AC,点O为△ABC外接圆的圆心,连结OC,过点B作AC的垂线,交⊙O于点D,交OC于点E,交AC于点F,连结AD和CD.
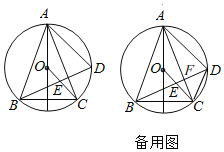
(1)若∠BAC=2α,则∠BDA= (用含α的代数式表示).
(2)①求证:OC∥AD;
②若E为OC的中点,求![]() 的值.
的值.
(3)若x=![]() ,y=
,y=![]() ,求y关于x的函数关系式.
,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
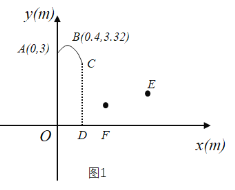
【题目】在篮球比赛中,东东投出的球在点A处反弹,反弹后球运动的路线为抛物线的一部分(如图1所示建立直角坐标系),抛物线顶点为点B.
(1)求该抛物线的函数表达式.
(2)当球运动到点C时被东东抢到,CD⊥x轴于点D,CD=2.6m.
①求OD的长.
②东东抢到球后,因遭对方防守无法投篮,他在点D处垂直起跳传球,想将球沿直线快速传给队友华华,目标为华华的接球点E(4,1.3).东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1=﹣2(t﹣0.5)2+2.7(0≤t≤1);小戴在点F(1.5,0)处拦截,他比东东晚0.3s垂直起跳,其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图2所示(其中两条抛物线的形状相同).东东的直线传球能否越过小戴的拦截传到点E?若能,东东应在起跳后什么时间范围内传球?若不能,请说明理由(直线传球过程中球运动时间忽略不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情防控期间,学校开学初购进A、B两种消毒液,购买A种消毒液花费2500元,购买B种消毒液花费2000元,且A种消毒液数量是B种消毒液数量的2倍,一桶B种消毒液比一桶A种消毒液贵30元.
(1)求购买一桶A种、一桶B种消毒液各需多少元?
(2)为了加强防控,学校准备再次购买A、B两种消毒液共50桶,A种消毒液售价比第一次提高了8%,B种消毒液按第一次售价的9折出售,如果此次购买总费用不超过3260元,那么学校此次最多可购买多少桶B种消毒液?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com