
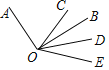
【题目】如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与∠BOD互余,其中正确的有______(只填写正确结论的序号).
【答案】①②④
【解析】
由角平分线将角分成相等的两部分.结合选项得出正确结论.
解:①∵OB,OD分别平分∠COD,∠BOE,
∴∠COB=∠BOD=∠DOE,
设∠COB=x,
∴∠COD=2x,∠BOE=2x,
∴∠COD=∠BOE,
故①正确;
②∵∠COE=3x,∠BOD=x,
∴∠COE=3∠BOD,
故②正确;
③∵∠BOE=2x,∠AOC=90°-x,
∴∠BOE与∠AOC不一定相等,
故③不正确;
④∵OA⊥OB,
∴∠AOB=∠AOC+∠COB=90°,
∵∠BOC=∠BOD,
∴∠AOC与∠BOD互余,
故④正确,
∴本题正确的有:①②④;
故答案为:①②④.


科目:初中数学 来源: 题型:
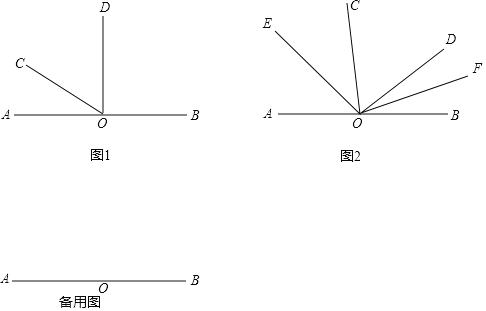
【题目】已知:如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角时,3∠AOC=∠BOD,求∠COD的度数;
(2)若∠COD保持在(1)中的大小不变,它绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)若∠COD从(1)中的位置开始,边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转(当其中一边与OB重合时都停止旋转),OM、ON分别平分∠BOC、∠BOD.
求:①运动多少秒后,∠COD=10°;
②运动多少秒后,∠COM=∠BON.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点.
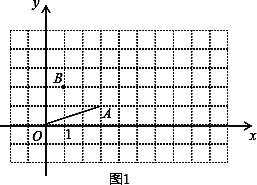
(1)已知点A(3,1),连结OA,作如下探究:
探究一:平移线段OA,使点O落在点B.设点A落在点C,若点B的坐标为(1,2),请在图1中作出BC,点C的坐标是_________;
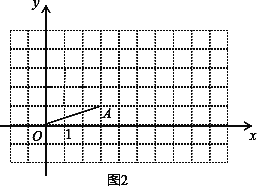
探究二:将线段OA绕点O逆时针旋转90°,设点A落在点D.则点D的坐标是_______.
(2) 已知四点O(0,0),A (a,b), C,B(c,d),顺次连结O,A,C,B.
若所得到的四边形是正方形,请直接写出a,b,c,d应满足的关系式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,反比例函数y=![]() 的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
的图象与一次函数y=k(x-2)的图象交点为A(3,2),B(x,y).
(1)求反比例函数与一次函数的解析式及B点坐标;
(2)若C是y轴上的点,且满足△ABC的面积为10,求C点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
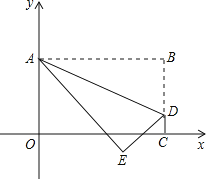
(1)当m=3时,点B的坐标为 ,点E的坐标为 ;
(2)随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.
(3)如图,若点E的纵坐标为-1,且点(2![]() ,a)落在△ADE的内部,求a的取值范围.
,a)落在△ADE的内部,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3 cm,P、Q分别从B、A出发沿BC,AD方向运动,P点的运动速度是1 cm/秒,Q点的运动速度是2 cm/秒。连接AP并过Q作QE⊥AP垂足为E。
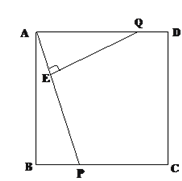
(1)求证:△ABP∽△QEA ;
(2)当运动时间t为何值时,△ABP≌△QEA;
(3)设△QEA的面积为y,用运动时间t表示△QEA的面积y。(不要求考虑t的取值范围)
(提示:解答(2)(3)时可不分先后)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,AB:BC=3:2,∠DCB=60°,点E在AB上,BE=2AE,点F为BC的中点,DP⊥AF,DQ⊥CE,则DP:DQ=( )
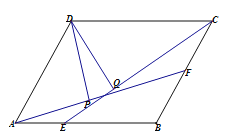
A.3:4B.1:1C.![]() :
:![]() D.3:
D.3:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )
①有理数包括正有理数和负有理数; ②绝对值等于它本身的数是非负数;③若|b|=|﹣5|,则b=-5 ; ④当b=2时,5﹣|2b﹣4|有最小值是5;⑤若![]() 、
、![]() 互为相反数,则
互为相反数,则![]() ;⑥
;⑥![]() 是关于
是关于![]() 、
、![]() 的六次三项式.
的六次三项式.
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com