
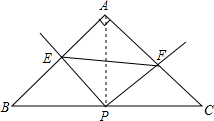
 如图测,在△ABC中,AB=AC,∠BAC=90°,直角EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F
如图测,在△ABC中,AB=AC,∠BAC=90°,直角EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F分析 (1)根据全等三角形的判定定理ASA证明△AEP≌△CFP,然后由全等三角形的对应边相等求得AE=CF;
(2)根据全等三角形的性质得到PE=PF,由于∠EPF=90°,即可得到结论;
(3)利用“割补法”求得S四边形AEPF=S△AEP+S△AFP,然后利用(1)的结果知S△AEP=S△CPF,于是得到S四边形AEPF=S△APC=$\frac{1}{2}$S△ABC.
解答 证明:(1)在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴AP=PC=BP(直角三角形斜边上的中线是斜边长的一半);
在直角三角形ABP中,∠B=∠BAP=45°;
在直角三角形APC中,∠PAC=∠C=45°;
∴∠EAP=∠C=45°;
∵∠FPE=∠APC=90°,
∴∠CPF=∠APE;
在△AEP与△CPF中,
$\left\{\begin{array}{l}{∠EAP=∠C=45°}\\{AP=CP}\\{∠CPF=∠APE}\end{array}\right.$,
∴△AEP≌△CPF(ASA),
∴AE=CF,
∴AC=AF+AE;
(2)∵△AEP≌△CPF,
∴PE=PF,
∵∠EPF=90°,
∴△EPF为等腰直角三角形;
(3)∵△AEP≌△CPF,
∴S△AEP=S△CPF(全等三角形的面积相等);
又∵S四边形AEPF=S△AEP+S△AFP,
∴S四边形AEPF=S△APC=$\frac{1}{2}$S△ABC;
即S四边形AEPF=$\frac{1}{2}$S△ABC,
∵AP=2,
∴BC=2AP=4,
∴S四边形AEPF=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×2×4=2.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=1,c=2 | B. | a=1,b=-1,c=-2 | C. | a=1,b=1,c=-2 | D. | a=1,b=-1,c=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:
如图,已知抛物线T:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线T上部分点的横坐标对应的纵坐标如下:| x | … | -3 | -2 | 1 | 2 | … |
| y | … | -$\frac{5}{2}$ | -4 | -$\frac{5}{2}$ | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:填空题
超市决定招聘广告策划员一名,某应聘者三项素质测试的成绩如下表所示:
测试项目 | 创新能力 | 综合知识 | 语言表达 |
测试成绩(分) | 82 | 70 | 90 |
将创新能力、综合知识和语言表达三项测试成绩按50%,30%,20%的比例计入总成绩,则该应聘者的总成绩是__________分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com