
分析 连接O1A、O2A,由相交两圆的性质得出O1O2垂直平分AB,得出∠ACO1=∠ACO2=90°,AC=$\frac{1}{2}$AB=6cm,由勾股定理求出O1C和O2C,O1O2=O1C+O2C,即可得出结果.
解答 解:连接O1 A、O2 A,如图所示: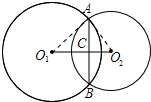
∵⊙O1与⊙O2相交于A、B,
∴O1O2垂直平分AB,
∴∠ACO1=∠ACO2=90°,AC=$\frac{1}{2}$AB=6cm,
由勾股定理得:O1C=$\sqrt{{O}_{1}{A}^{2}-A{C}^{2}}$=$\sqrt{1{5}^{2}-{6}^{2}}$=3$\sqrt{21}$(cm),O2C=$\sqrt{{O}_{2}A-A{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8(cm),
∴O1O2=O1 C+O2C=3$\sqrt{21}$+8(cm),
即两圆的圆心距为(3$\sqrt{21}$+8)cm.
点评 本题考查了相交两圆的性质、勾股定理;熟练掌握相交两圆的性质,运用勾股定理进行计算是解决问题的关键.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:选择题
 如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )
如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是( )| A. | 75°36′ | B. | 75°12′ | C. | 74°36′ | D. | 74°12′ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com