
分析 设$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m,从而得出m2=2-$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=2-m,解关于m的方程即可,m是非负数,再取舍即可.
解答 解:设$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m,
∴m2=2-$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$,
∴m2=2-m,
∴m2+m-2=0,
∴m1=-2(舍),m2=1,
∵m是非负数,
∴m=1,
∴$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$的值为1.
点评 本题考查了二次根式的化简求值,设出$\sqrt{2-\sqrt{2-\sqrt{2-\sqrt{…}}}}$=m是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
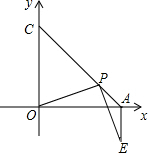 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.
如图,在△ABC中,∠ABC=100°,CE平分∠ACB交AB于点E,点D在AC上,且∠CBD=20°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com