
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
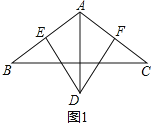
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
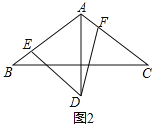
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
【答案】(1)见解析;![]() ,理由见解析.
,理由见解析.
【解析】
(1)连接BD,证△ABD是等边三角形,得∠ABD=∠BDA=∠DAB=60,再证△BDE≌△ADF(AAS),AF=BE,故AB=AE+BE;
(2)线段AE,AF,AD之间的数量关系为:![]() ,思路如下:
,思路如下:
连接BD,模仿(1)证△BDE≌△ADF(AAS),得![]() ,所以
,所以![]() .
.
∵在△ABC中,AB=AC,AD⊥BC,∠BAC=120
∴∠BAD=∠FAD=60
∵AD=AB
∴△ABD是等边三角形
∴∠ABD=∠BDA=∠DAB=60
∵DE⊥AB,DF⊥AC
∴∠BED=∠DFA=90
在△BDE和△ADF中,
∠BED=∠DFA,∠EBD=∠FAD,BD=DA,
∴△BDE≌△ADF(AAS)
∴AF=BE
∴AB=AE+BE
∴AB=AE+AF
![]() 解:线段AE,AF,AD之间的数量关系为:
解:线段AE,AF,AD之间的数量关系为:![]() ,理由如下:
,理由如下:
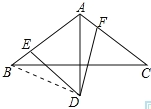
连接BD,如图所示:
![]() ,
,![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 与
与![]() 中,
中,
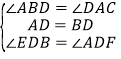 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】以下四个命题:①全等三角形的面积相等;②最小角等于50°的三角形是锐角三角形;③等腰△ABC中,D是底边BC上一点,E是一腰AC上的一点,若∠BAD=60°且AD=AE,则∠EDC=30°;④将多项式![]() 因式分解,其结果为-y(2x+1)(x-3).其中正确命题的序号为___________.
因式分解,其结果为-y(2x+1)(x-3).其中正确命题的序号为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
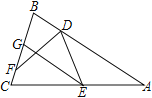
【题目】如图,在△ABC中,AB=AC,D、E分别为AB、AC上的点,∠BDE、∠CED的平分线分别交BC于点F、G,EG∥AB.若∠BGE=110°,则∠BDF的度数为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A,B,O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为 . 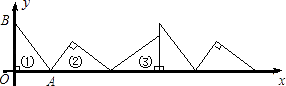
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是 ( )

A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选定点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com