
(2011•陕西)如图,二次函数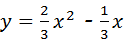 的图象经过△AOB的三个顶点,其中A(﹣1,m),B(n,n)
的图象经过△AOB的三个顶点,其中A(﹣1,m),B(n,n)
(1)求A、B的坐标;
(2)在坐标平面上找点C,使以A、O、B、C为顶点的四边形是平行四边形.
①这样的点C有几个?
②能否将抛物线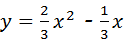 平移后经过A、C两点,若能,求出平移后经过A、C两点的一条抛物线的解析式;若不能,说明理由.
平移后经过A、C两点,若能,求出平移后经过A、C两点的一条抛物线的解析式;若不能,说明理由.
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(陕西卷)数学解析版 题型:解答题
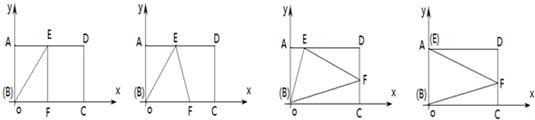
(2011•陕西)如图①,在矩形ABCD中,将矩形折叠,使B落在边AD(含端点)上,落点记为E,这时折痕与边BC或者边CD(含端点)交于F,然后展开铺平,则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
(1)由“折痕三角形”的定义可知,矩形ABCD的任意一个“折痕△BEF”是一个 三角形
(2)如图②、在矩形ABCD中,AB=2,BC=4,,当它的“折痕△BEF”的顶点E位于AD的中点时,画出这个“折痕△BEF”,并求出点F的坐标;
(3)如图③,在矩形ABCD中,AB=2,BC=4,该矩形是否存在面积最大的“折痕△BEF”?若存在,说明理由,并求出此时点E的坐标?若不存在,为什么?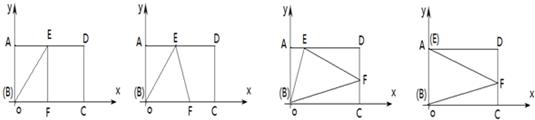
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(陕西卷)数学解析版 题型:解答题
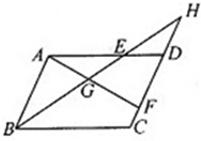
(2011•陕西)如图,在△ABC中,∠B=60°,⊙O是△ABC外接圆,过点A作⊙O的切线,交CO的延长线于P点,CP交⊙O于D
(1)求证:AP=AC;
(2)若AC=3,求PC的长.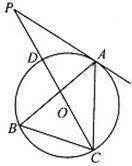
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com