
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
【答案】(1)①![]() ;
;![]() ;
;
②所填的条件是:![]() .
.
证明:在![]() 中,
中,![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
又![]() ,
,![]() ,
,
![]() .
.
![]() ,
,![]() .
.
又![]() ,
,![]() .
.
(2)![]() .
.
【解析】
(1)①由∠BCA=90°,∠α=90°可得∠CBE+∠BCE=90°,∠BCE+∠ACD=90°,可推得∠CBE=∠ACD,且已知CA=CB,∠BEC=∠CFA,所以△BEC≌△CDA,可得BE=CF,EC=AF;又因为EF=CF-CE,所以EF=|BE-AF|;
②只有满足△BEC≌△CDA,才有①中的结论,即∠BCE=∠CAF,∠CBE=∠FCA;由三角形内角和等于180°,可知∠α+∠BCE+∠CBE=180°,即∠α+∠BCE+∠FCA=180°,即可得到∠α+∠BCA=180°.
(2)只要通过条件证明△BEC≌△CFA(可通过ASA证得),可得BE=CF,EC=AF,即可得到EF=EC+CF=BE+AF.


科目:初中数学 来源: 题型:
【题目】【数学概念】
若四边形ABCD的四条边满足AB![]() CD
CD![]() AD
AD![]() BC,则称四边形ABCD是和谐四边形.
BC,则称四边形ABCD是和谐四边形.
【特例辨别】
(1)下列四边形:①平行四边形,②矩形,③菱形,④正方形.其中一定是和谐四边形的是________.
【概念判定】
(2)如图①,过⊙O外一点P引圆的两条切线PS、PT,切点分别为A、C,过点P 作一条射线PM,分别交⊙O于点B、D,连接AB、BC、CD、DA.求证:四边形ABCD是和谐四边形.

【知识应用】
(3)如图②,CD是⊙O的直径,和谐四边形ABCD内接于⊙O,且BC![]() AD.请直接写出AB与CD的关系.
AD.请直接写出AB与CD的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作甲、乙两种窗户边框,已知同样用12米材料制成甲种边框的个数比制成乙种边框的个数少1个,且制成一个甲种边框比制成一个乙种边框需要多用![]() 的材料.
的材料.
(1)求制作每个甲种边框、乙种边框各用多少米材料?
(2)如果制作甲、乙两种边框的材料共640米,要求制作乙种边框的数量不少于甲种边框数量的2倍,求应最多安排制作甲种边框多少个(不计材料损耗)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处时,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE 是菱形吗?(填“可能”或“不可能”)

查看答案和解析>>
科目:初中数学 来源: 题型:
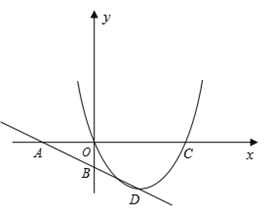
【题目】如图,直线![]() 与
与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,抛物线
轴交于点B,抛物线![]() 经过原点和点C(4,0),顶点D在直线AB上。
经过原点和点C(4,0),顶点D在直线AB上。
(1)求这个抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使得以P、C、D为顶点的三角形与△ACD相似。若存在,请求出点P的坐标;若不存在,请说明理由;
(3)点Q是![]() 轴上方的抛物线上的一个动点,若
轴上方的抛物线上的一个动点,若![]() ,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
,⊙M经过点O,C,Q,求过C点且与⊙M相切的直线解析式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com