
����Ŀ����ƽ��ֱ������ϵ�У�O������ԭ�㣬ABCD�Ķ���A������Ϊ����2��0������D������Ϊ��0��2 ![]() ������B��x����������ϣ���EΪ�߶�AD���е㣮
������B��x����������ϣ���EΪ�߶�AD���е㣮
��1����ͼ1�����DAO�Ĵ�С���߶�DE�ij���
��2������E��ֱ��l��x�ύ�ڵ�F��������DC���ڵ�G������OE����OEF���ǡ�OEF����ֱ��OE�ԳƵ�ͼ�Σ���ֱ��EF��������DC�Ľ���ΪH����EHC�����Ϊ3 ![]() ��
��
����ͼ2������G�ڵ�H�����ʱ����GH��DG�ij���
�ڵ���G�ڵ�H���Ҳ�ʱ�����F�����ֱ꣨��д��������ɣ���
���𰸡�
��1���⣺��A����2��0����D��0��2 ![]() ��
��
��AO=2��DO=2 ![]() ��
��
��tan��DAO= ![]() =
= ![]() ��
��
���DAO=60�㣬
���ADO=30�㣬
��AD=2AO=4��
�ߵ�EΪ�߶�AD�е㣬
��DE=2��
��2���⣺����ͼ2��
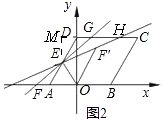
����E��EM��CD��
��CD��AB��
���EDM=��DAB=60�㣬
��EM=DEsin60��= ![]() ��
��
��GH=6��
��CD��AB��
���DGE=��OFE��
�ߡ�OEF���ǡ�OEF����ֱ��OE�ĶԳ�ͼ�Σ�
���OEF��ա�OEF��
���OFE=��OF��E��
�ߵ�E��AD���е㣬
��OE= ![]() AD=AE��
AD=AE��
�ߡ�EAO=60�㣬
���EAO�ǵȱ������Σ�
���EOA=60�㣬��AEO=60�㣬
�ߡ�OEF��ա�OEF��
���EOF��=��EOA=60�㣬
���EOF��=��AEO��
��AD��OF�䣬
���OF��E=��DEH��
���DEH=��DGE��
�ߡ�DEH=��EDG��
���DHE�ס�DEG��
�� ![]() ��
��
��DE2=DG��DH��
��DG=x����DH=x+6��
��4=x��x+6����
��x1=��3+ ![]() ��x2=��3��
��x2=��3�� ![]() ��
��
��DG=��3+ ![]() ��
��
����ͼ3��
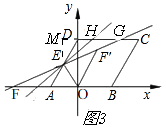
����E��EM��CD��
��CD��AB��
���EDM=��DAB=60�㣬
��EM=DEsin60��= ![]() ��
��
��GH=6��
��CD��AB��
���DHE=��OFE��
�ߡ�OEF���ǡ�OEF����ֱ��OE�ĶԳ�ͼ�Σ�
���OEF��ա�OEF��
���OFE=��OF��E��
�ߵ�E��AD���е㣬
��OE= ![]() AD=AE��
AD=AE��
�ߡ�EAO=60�㣬
���EAO�ǵȱ������Σ�
���EOA=60�㣬��AEO=60�㣬
�ߡ�OEF��ա�OEF��
���EOF��=��EOA=60�㣬
���EOF��=��AEO��
��AD��OF�䣬
���OF��E=��DEH��
���DEG=��DHE��
�ߡ�DEG=��EDH��
���DGE�ס�DEH��
�� ![]() ��
��
��DE2=DG��DH��
��DH=x����DG=x+6��
��4=x��x+6����
��x1=��3+ ![]() ��x2=��3��
��x2=��3�� ![]() ��
��
��DH=��3+ ![]() ��
��
��DG=3+ ![]()
��DG=AF=3+ ![]() ��
��
��OF=5+ ![]() ��
��
��F����5�� ![]() ��0����
��0����
����������1�����ݵ�A��������D�����꣬��Rt��AOD�У����ý�ֱ����������������ۡ�
��2�����ɣ�1����֪��DAO=60�㣬���Ӹ����ߣ�����E��EM��CD�����ý�ֱ�������ο����EM��GH�ij���������֪��֤����OEF��ա�OEF���ɵó�����ȣ���E��AD���е㣬�õ���EAO�ǵȱ������Σ���֤����DHE�ס�DEG���ó���Ӧ�߳ɱ�������DG=x����DH=x+6���������̣�������̵Ľ⼴�ɣ���Ҫ���F�����꣬������OF�ij����ⷨ����������DG��DG=AF���������OF�ij����Ӷ������F�����ꡣ
�����㾫�����������⣬������Ҫ�˽�ƽ���ı��ε�����(ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ��)����Ҫ�������������ε��ж�������(���������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��)�����֪ʶ���Ǵ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬˫����
���е㣬˫����![]() ����
����![]() ��
��![]() ���㣮
���㣮

��1����![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2����ͼ1����![]() ��
��![]() ���ϣ����ı���
���ϣ����ı���![]() ��ƽ���ı��Σ����
��ƽ���ı��Σ����![]() �����ꣻ
�����ꣻ
��3����ͼ2���ڣ�2���������£�����![]() ��˫����
��˫����![]() �ϣ���
�ϣ���![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊƽ���ı��Σ���������Ҫ������е�
Ϊ������ı���Ϊƽ���ı��Σ���������Ҫ������е�![]() ��
��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУΪ�˽�ѧ�������š����������������֡�Ϸ������ӽ�Ŀ��ϲ����������ó����ķ��������꼶ѡȡ��һ�����ͬѧ��ͨ���ʾ����飬�ռ����ݡ��������ݣ�����������������ͳ��ͼ�����������������������ͳ��ͼ�������ݣ��ش��������⣺

��1�����꼶��������ѧ��_____�ˣ�ͼ��![]() ______��
______��![]() ______��������ͳ��ͼ�У�������������ӽ�Ŀ��Ӧ��Բ�Ľ�Ϊ��______.
______��������ͳ��ͼ�У�������������ӽ�Ŀ��Ӧ��Բ�Ľ�Ϊ��______.
��2����ȫ����ͳ��ͼ��
��3�����ݳ�������Ľ���������У1750��ѧ���д�Լ�ж�����ϲ�������֡�����ӽ�Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ尴��ͼ�ٵ�λ�ðڷţ�����DEF�Ƶ�A��F����ʱ����ת60��õ���ͼ�ڣ����CG=6 ![]() ����AC���ǣ� ��
����AC���ǣ� ��
A.6+2 ![]()
B.9
C.10
D.6+6 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��A=40�㣬��ABC����ǡ�CBD��ƽ����BE��AC���ӳ����ڵ�E��
��1�����CBE�Ķ�����
��2������D��DF��BE����AC���ӳ����ڵ�F�����F�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�����Σ�AC=8��DB=6��DH��AB��H����DH=�� ��
A.![]()
B.![]()
C.12
D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������ABC�У�AB=AC����D,E�ֱ��ڱ�AB��AC�ϣ���AD=AE������BE��CD�����ڵ�F.

(1)��֤����ABE����ACD��
(2)��֤������A��F��ֱ�ߴ�ֱƽ���߶�BC.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵����
�ٸ�������������Ϊ������
��1��ƽ����������������1��
��4��ƽ�������������� ![]() ��
��
�ܻ�Ϊ�෴��������������������Ϊ�෴����
��ȷ���У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У�����y= ![]() ��x��0����ͼ����һ�κ���y=kx��k��ͼ��Ľ���ΪA��m��2����
��x��0����ͼ����һ�κ���y=kx��k��ͼ��Ľ���ΪA��m��2����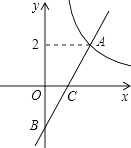
��1����һ�κ����Ľ���ʽ��
��2����һ�κ���y=kx��k��ͼ����y�ύ�ڵ�B������P��x����һ�㣬�������PAB�������4��ֱ��д��P������꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com