
【题目】已知Rt△ABC中,∠B=90°
(1)根据要求作图(尺规作图,保留作图痕迹,不写画法)
①作∠BAC的平分线AD交BC于D;
②作线段AD的垂直平分线交AB于E,交AC于F,垂足为H;
③连接ED.
(2)在(1)的基础上写出一对相似比不为1的相似三角形和一对全等三角形:
_________________________;__________________________.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为______;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为_______.
(2)利用(1)中求不等式解集的步骤,求不等式x2﹣2x+1≥4的解集.
①构造界点,画出图象;
②求得界点,标志所需;
③借助图象,写出解集


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E,F分别平行四边形ABCD是的边BC,AD上的点,点E是线段BC的中点,且AE=BE,CF=FD,tanB=![]() ,若CD=4,求四边形AECF的周长.
,若CD=4,求四边形AECF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,求
,求![]() 的最小值.
的最小值.
爱思考的小思想到了一种方法:先用![]() 表示
表示![]() 得:
得:![]() _____;
_____;
再把![]() 代入
代入![]() 得到:
得到:![]() ______;
______;
再利用配方法得到:![]() (
(![]() _____)
_____)![]() +______;
+______;
根据完全平方式的非负性,就得到了![]() 的最小值是______.
的最小值是______.
请你补充完成小思的解答过程:
(2)根据小思的方法,请你求出:当![]() 时,求出
时,求出![]() 的最小值.
的最小值.
(3)但是假如变成![]() ,求
,求![]() 的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
的最小值的时候小思的方法就不好用了,因此喜欢面对挑战的小喻同学想到了一种叫增量代换法:
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
则 ,
,
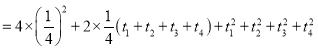 ,
,
![]() .
.
故![]() 的最小值是
的最小值是![]() .
.
参考小喻的方法,当![]() 时,
时,
求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
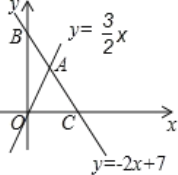
【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=![]() x相交于点A.
x相交于点A.
(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,这样的式子我们可以将其进一步化简
一样的式子,这样的式子我们可以将其进一步化简![]() =
=![]() ,
,![]() ,
,![]() 以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
(1)化简:![]() ;
;
(2)若a是![]() 的小数部分,求
的小数部分,求![]() 的值;
的值;
(3)矩形的面积为3![]() +1,一边长为
+1,一边长为![]() ﹣2,求它的周长.
﹣2,求它的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com