
【题目】如图,已知四边形ABCD是菱形,DF⊥AB于点F,BE⊥CD于点E.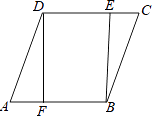
(1)求证:AF=CE;
(2)若DE=2,BE=4,求sin∠DAF的值.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∵DF⊥AB,BE⊥CD,
∴DF∥BE,
∴四边形BEDF是平行四边形,
∴BF=DE,
∴AF=CE;
(2)证明:∵DE=2,BE=4,
∴设AD=x,则AF=x﹣2,DF=BE=4,
在Rt△DAF中,x2=42+(x﹣2)2,
解得x=5,
∴sin∠DAF= ![]() =
= ![]() .
.
【解析】(1)判定四边形BEDF是平行四边形,根据平行四边形的对边相等,即可证得;(2)要求sin∠DAF,须求斜边BC的长,即菱形的边长,可在Rt△DAF中建立方程,求出AD,按照正弦定义即可求出.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知l1//l2,射线MN分别和直线l1,l2交于点A,B,射线ME分别和直线l1,l2交于点C,D,点P在射线MN上运动(P点与A,B,M三点不重合),设∠PDB=α ,∠PCA=β ,∠CPD=γ .
(1)如果点P在A,B两点之间运动时,α,β,γ之间有何数量关系?请说明理由;
(2)如果点P在A,B两点之外运动时,α,β,γ之间有何数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ),B(4,0)两点.
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径画弧,分别交直线l1和l2于B、C两点,连接AC、BC,若∠ABC=65°,则∠1的度数是( )

A. 35° B. 50° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
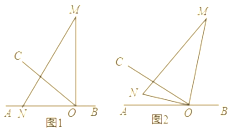
【题目】如图,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板 (∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方,将如图中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周。
(1)几秒后ON与OC重合?
(2)如图,经过t秒后,MN∥AB,求此时t的值。
(3)若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,那么经过多长时间OC与OM重合?请画图并说明理由。
(4)在(3)的条件下,求经过多长时间OC平分∠MOB?请画图并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△PQR在直角坐标系中的位置如图所示:
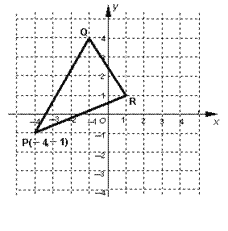
(1) 求出△PQR的面积;
(2) 画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;
(3)连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.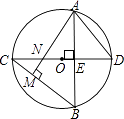
(1)求证:AD=AN;
(2)若AB=4 ![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E是AC的中点,OE交CD于点F.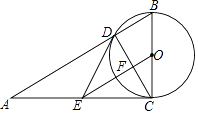
(1)若∠BCD=36°,BC=10,求BD的长;
(2)判断直线DE与⊙O的位置关系,并说明理由;
(3)求证:2CE2=ABEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com