
 已知二次函数y=$\frac{1}{2}$x2+x-$\frac{3}{2}$.
已知二次函数y=$\frac{1}{2}$x2+x-$\frac{3}{2}$.分析 (1)根据配方法的步骤即可解决.
(2)利用描点法画出函数图象即可.
(3)①根据图象即可判断.
②利用图象法解决即可.
③利用图象法即可解决.
解答 解:(1)y=$\frac{1}{2}$x2+x-$\frac{3}{2}$化成y=$\frac{1}{2}$(x2+2x+1-1)-$\frac{3}{2}$=$\frac{1}{2}$(x+1)2-2.
(2)函数图象如图所示,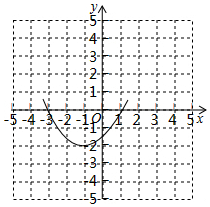
(3)①由图象可知当x>-1时,y随x的增大而增大.
故答案为x>-1.
②x=-2时,y=-$\frac{3}{2}$,x=2时,y=$\frac{5}{2}$,x=-1时,y=-2,
∴当-2<x<2时,则y的取值范围是-2≤y<$\frac{5}{2}$.
故答案为-2≤y$\frac{5}{2}$
③由图象可知m<-2时,方程$\frac{1}{2}$x2+x-$\frac{3}{2}$=m没有实数解.
故答案为m<-2.
点评 本题考查二次函数与x轴的交点,函数的增减性等知识,解题的关键是熟练掌握二次函数的性质,学会利用图象解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
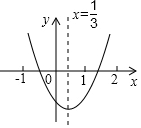 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①abc>0;②a-b+c>0;③4a+2b+c<0;④2a-3b=0;⑤c-4b>0,其中正确的有( )
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①abc>0;②a-b+c>0;③4a+2b+c<0;④2a-3b=0;⑤c-4b>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
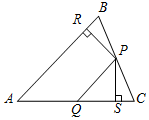 如图,在△ABC中,点P为BC中点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠QPC=∠C,PR=PS,下面三个结论:①AS=AR②△BRP≌△CSP③QP∥AR中,正确的结论有①③.
如图,在△ABC中,点P为BC中点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,∠QPC=∠C,PR=PS,下面三个结论:①AS=AR②△BRP≌△CSP③QP∥AR中,正确的结论有①③.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
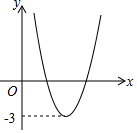 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k 的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,则k 的取值范围是( )| A. | k<-3 | B. | k>-3 | C. | k<3 | D. | k>3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水果经销商到水果种植基地采购葡萄,经销商一次性采购葡萄的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A),
某水果经销商到水果种植基地采购葡萄,经销商一次性采购葡萄的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com