
【题目】如图,矩形ABCD中,AC=4,AB=2,将矩形ABCD绕点A旋转得到矩形AB'C'D',使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C'上取点F,使B'F=AB.
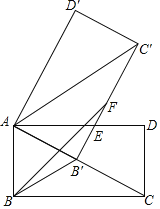
(1)求证:AE=C'E;
(2)求BF的长.
【答案】(1)见解析;(2)BF=![]() +
+![]() .
.
【解析】
(1)在直角三角形ABC中,由AC=2AB,得到∠ACB=30°,再由折叠的性质得到一对角相等,利用等角对等边即可得证;
(2)连接AF,过A作AM⊥BF,可得△AB′F是等腰直角三角形,△AB′B为等边三角形,分别利用三角函数定义求出MF与AM,根据AM=BM,即BM+MF=BF即可求出.
(1)证明:∵在Rt△ABC中,AC=2AB,
∴∠ACB=∠AC′B′=30°,∠BAC=60°,
由旋转可得:AB′=AB,∠B′AC′=∠BAC=60°,
∴∠EAC′=∠AC′B′=30°,
∴AE=C′E;
(2)连接AF,过A作AM⊥BF,可得△AB′F是等腰直角三角形,△AB′B为等边三角形,
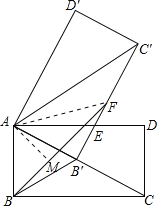
∴∠AFB′=45°,
∴∠AFM=30°,∠ABF=45°,
在Rt△AMF中,AM=BM=ABcos∠ABM=2×![]() ,
,
在Rt△AMF中,MF=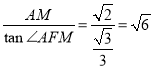 ,
,
则BF=![]() +
+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
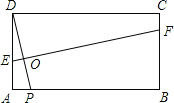
【题目】如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=![]() ,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
(1)当![]() =0时,折痕EF的长为 ;当点E与点A重合时,折痕EF的长为 ;
=0时,折痕EF的长为 ;当点E与点A重合时,折痕EF的长为 ;
(2)请写出使四边形EPFD为菱形的![]() 的取值范围,并求出当
的取值范围,并求出当![]() =2时菱形的边长;
=2时菱形的边长;
(3)令EF2=![]() ,当点E在AD、点F在BC上时,写出
,当点E在AD、点F在BC上时,写出![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 取最大值时,判断△EAP与△PBF是否相似?若相似,求出
取最大值时,判断△EAP与△PBF是否相似?若相似,求出![]() 的值;若不相似,请说明理由.温馨提示:用草稿纸折折看,或许对你有所帮助哦!
的值;若不相似,请说明理由.温馨提示:用草稿纸折折看,或许对你有所帮助哦!
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好街坊橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共 30 台,用去了 5520 元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过 8850 元的资金采购电饭煲和电压锅共 50 台,且电饭煲的利润不少于电压锅的利润的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为12的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 边上的动点,且始终保持
边上的动点,且始终保持![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
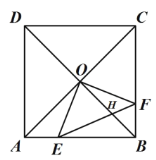
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在运动的过程中,![]() 是否存在最大值?若存在,请求出
是否存在最大值?若存在,请求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
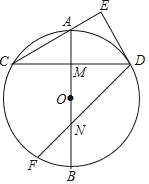
【题目】如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.
(1)连接AD,则∠OAD= °;
(2)求证:DE与⊙O相切;
(3)点F在![]() 上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
上,∠CDF=45°,DF交AB于点N.若DE=3,求FN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
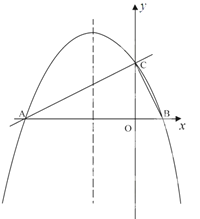
【题目】如图,在平面直角坐标系xoy中,直线![]() 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com