

���� ��1��������EG��AB��FH��AB������ƽ���ߵ����ʿɵá�ABE+��CDE=280�㣬�����ý�ƽ���ߵĶ���õ���ABF+��CDF=140�㣬�Ӷ��õ���BFD�Ķ�������2��������֪�õ���ABE=6��ABM����CDE=6��CDM���ɣ�1���á�ABE+��CDE=360��-��E����M=��ABM+��CDM���������������ɣ�
��3���ɣ�2���ķ����ɵõ�2n��M+��E=360�㣬����E=m�����ɵ�$��M=\frac{360��-m��}{2n}$��
��� �⣺��1����EG��AB��FH��AB��
��AB��CD��
��EG��AB��FH��CD��
���ABF=��BFH����CDF=��DFH����ABE+��BEG=180�㣬��GED+��CDE=180�㣬
���ABE+��BEG+��GED+��CDE=360��
�ߡ�BED=��BEG+��DEG=80�㣬
���ABE+��CDE=280�㣬
�ߡ�ABF�͡�CDF�Ľ�ƽ�����ཻ��E��
���ABF+��CDF=140�㣬
���BFD=��BFH+��DFH=140�㣻
��2���ߡ�ABM=$\frac{1}{3}$��ABF����CDM=$\frac{1}{3}$��CDF��
���ABF=3��ABM����CDF=3��CDM��
�ߡ�ABE���CDE�����ǵĽ�ƽ�����ཻ�ڵ�F��
���ABE=6��ABM����CDE=6��CDM��
��6��ABM+6��CDM+��E=360�㣬
�ߡ�M=��ABM+��CDM��
��6��M+��E=360�㣮
��3���ɣ�2�����ۿɵã�
2n��ABM+2n��CDM+��E=360�㣬��M=��ABM+��CDM��
��ã�$��M=\frac{360��-m��}{2n}$��
�ʴ�Ϊ��$��M=\frac{360��-m��}{2n}$
���� ������Ҫ������ƽ���ߵ����ʺ��ı��ε��ڽǺͣ��ؼ�����������ֱ��ƽ��ͬλ����ȣ��ڴ�����ȣ�ͬ���ڽǻ��������ʣ�


 �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
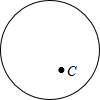 ��ͼ����֪��O��ֱ��Ϊ10����C��Բ��һ�㣬��OC=3��
��ͼ����֪��O��ֱ��Ϊ10����C��Բ��һ�㣬��OC=3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | -2 | C�� | 3 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
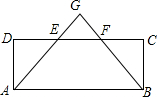 ��ͼ���ھ���ABCD�У�E��FΪ��CD�ϵ����㣬��DE=EF=FC������AE��BF�����ӳ�AE��BF�ཻ��G
��ͼ���ھ���ABCD�У�E��FΪ��CD�ϵ����㣬��DE=EF=FC������AE��BF�����ӳ�AE��BF�ཻ��G�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10����������$\root{3}{10}$ | B�� | -2��4��һ��ƽ���� | ||
| C�� | $\frac{4}{9}$��ƽ������$\frac{2}{3}$ | D�� | 0.01������ƽ������0.1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ1���ڡ�ABC�У���C=90�㣬AB=1����A=������cos��=$\frac{AC}{AB}=AC$���ֽ���ABC��AC�۵����õ���ADC����ͼ2����֪B��C��D���㹲�ߣ���DAB=2��������0�㣼����45�㣩��
��ͼ1���ڡ�ABC�У���C=90�㣬AB=1����A=������cos��=$\frac{AC}{AB}=AC$���ֽ���ABC��AC�۵����õ���ADC����ͼ2����֪B��C��D���㹲�ߣ���DAB=2��������0�㣼����45�㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ���ö����Ϊϰ�ߣ�ij��ѧ��չ�˶������ı�����������ѡ������50ƪ���Ļ��ֽ��������ͳ�����£�
Ϊ���ö����Ϊϰ�ߣ�ij��ѧ��չ�˶������ı�����������ѡ������50ƪ���Ļ��ֽ��������ͳ�����£�| �ȼ� | �ɼ�����S��ʾ�� | Ƶ�� | Ƶ�� |
| һ�Ƚ� | 90��S��100 | 10 | a |
| ���Ƚ� | 80��S��90 | 16 | b |
| ���Ƚ� | 70��S��80 | c | 0.48 |
| �ϼ� | 50 | 1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com