
【题目】如果一个多位自然数的任意两个相邻数位上,左边数位上的数总比右边数位上的数小1,那么我们把这样的自然数叫做“相连数”,例如:234,4567,56789,......都是“相连数”.
(1)请直接写出最大的两位“相连数”与最小的三位“相连数”,并求它们的和;
(2)若某个“相连数”恰好等于其个位数的576倍,求这个“相连数”.
【答案】(1)212;(2)这个“相连数”为:3456;
【解析】
(1)根据题意得出数字,相加即可.
(2)先由题意得出x的范围,再分类讨论列出式子即可.
(1)由题意得:最大的两位“相连数”:89;最小的三位“相连数”:123;
它们的和:89+123=212;
(2)设这个“相连数”的个位数为x.
∵1≤x≤9
∴1×576≤这个“相连数”≤9×576=5211
∴这个数可能为三位数或四位数
①当这个数为三位数时:
100(x-2)+10(x-1)+x=576x
100x-200+10x-10+x=576x
465x=﹣210
x=![]()
不符合题意,舍去
②当这个数为四位数时:
1000(x-3)+100(x-2)+10(x-1)+x=576x
1000x-3000+100x-200+10x-10+x=576x
535x=3210
x=6
∴这个“相连数”为:3456


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
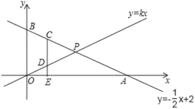
【题目】在平面直角坐标系中,一次函数![]() 的图象交
的图象交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,交直线
两点,交直线![]() 于
于![]() 。
。
(1)求点![]() 的坐标;
的坐标;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,点D,E分别在AC,BC上,且CD·BC=AC·CE,以E为圆心,DE长为半径作圆,⊙E经过点B,与AB,BC分别交于点F,G.
(1)求证:AC是⊙E的切线;
(2)若AF=4,CG=5,
①求⊙E的半径;
②若Rt△ABC的内切圆圆心为I,则IE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
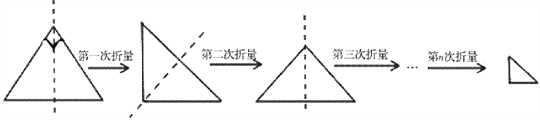
图1 图2 图3 图n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
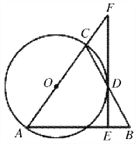
【题目】如图,在△ABC中,AB=AC,以AC为直径作![]() 交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证: EF与![]() 相切;
相切;
(2)若AE=6,![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣6,点B表示10,点C表示14,我们称点A和点C在数轴上相距20个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
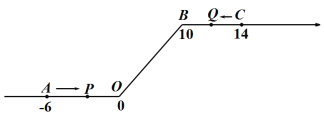
问:
(1)动点P从点A运动至C点需要时间为 秒;P、Q两点相遇时,求出相遇点M所对应的数是 ;
(2)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )

A. 甲正确,乙不正确B. 甲不正确,乙正确
C. 甲、乙都正确D. 甲、乙都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
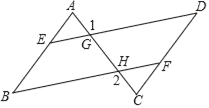
【题目】在括号内注明说理依据.如图已知∠B=∠D,∠1=∠2,试猜想∠A与∠C的大小关系,并说明理由.
解:猜想∠A=∠C
∵∠1=∠2 (已知)
∠1=∠EGC
∴∠2=∠EGC
∴BF∥DE
∴∠B=∠AED
∵∠B=∠D
∴∠AED=∠D (等量代换)
∴AB∥CD
∴∠A=∠C .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com