
【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3 ![]() ,BC=3
,BC=3 ![]() ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 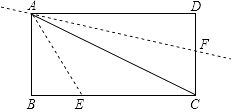
【答案】2 ![]()
【解析】解:∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵AB=3 ![]() ,BC=3
,BC=3 ![]() ,
,
∴tan∠BAC= ![]() =
= ![]() ,
,
∴∠BAC=60°,
∵把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,
∴∠BAE=∠CAE=30°,∠DAF=∠CAF,
∴∠EAP=∠EAC+∠FAC= ![]() BAD=45°,
BAD=45°,
过E作EP⊥AF于P,
此时,PE的值最小,
∵AB=3 ![]() ,∠B=90°,∠BAE=30°,
,∠B=90°,∠BAE=30°,
∴AE=2 ![]() ,
,
∵∠APE=90°,∠EAP=45°,
∴PE= ![]() AE=2
AE=2 ![]() .
.
∴PE的最小值为2 ![]() ,
,
所以答案是:2 ![]() .
.

【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的是( )

A. AE=BE B. DE⊥CE C. CD=AD+BC D. CD=AD+CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距3000米,甲、乙两人沿同一条路从A地到B地,l1,l2分别表示甲乙两人离开A地的距离y(m)与时间x(min)之间的关系,根据图象填空:
(1)甲出发 min后,乙才出发;
(2) 先到达终点
(3)乙的速度是 m/min.
(4)乙出发后 min追上甲,这时他们距离B地 m

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标中,直线l:y=﹣2x+6分别交两坐标于A、B两点,M是级段AB上一个动点,设点M的横坐标为x,△OMB的面积为S.
(1)写出S与x的函数关系式;
(2)当△OMB的面积是△OAB面积的![]() 时,求点M的坐标;
时,求点M的坐标;
(3)当△OMB是以OB为底的等腰三角形,求它的面积.
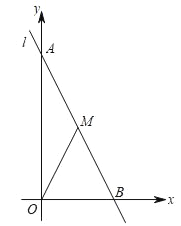
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某治安巡警分队常常在一条东西走向的街道上巡逻一天 下午,该巡警分队驾驶电动小汽车从位于这条街道上的某岗亭出发巡逻,如果规定向东为正,向西为负,他们行驶里程(单位: km)如下:![]() 问:
问:
(1)这辆小汽车完成巡逻后位于该岗亭的那一侧?距离岗亭有多少千米?
(2)已知这种电动小汽车平均每千米耗电![]() 度,则这天下午小汽车共耗电多少度?
度,则这天下午小汽车共耗电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.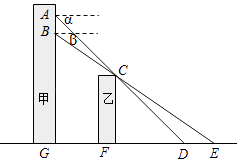
(1)求点A到地面的距离AG;
(2)求A,B之间的距离.(结果精确到0.1m)
(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com