
����Ŀ����ͼ������������y=![]() ��x��0����һ�κ���y=kx+6
��x��0����һ�κ���y=kx+6![]() ���ڵ�C��2��4
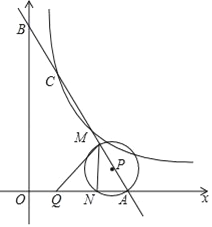
���ڵ�C��2��4![]() ����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ��
����һ�κ���ͼ������������ֱ��ڵ�A�͵�B������P�ӵ�A��������AB��ÿ��1����λ���ȵ��ٶ����B�˶���ͬʱ������Q�ӵ�O��������OA����ͬ���ٶ����A�˶����˶�ʱ��Ϊt�루0��t��6�����Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P��AB���ڵ�M����OA���ڵ�N������MN��MQ��
��1����m��k��ֵ��
��2����tΪ��ֵʱ����Q���N�غϣ�
��3������MNQ�����ΪS������S��t�ĺ�����ϵʽ��
���𰸡���1��m��8![]() ��k����
��k����![]() ����2��t=3����3��S=
����2��t=3����3��S=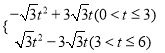
�������������������1�����ô���ϵ����ֱ�����m��k��
��2�������AB�������жϳ���MAN�ס�BAO�����ñ���ʽ�ó�AN��MN�����ɵó�ON������ON=OQ����������⼴�ɣ�
��3��������������������ε������ʽ���ɵó����ۣ�
�⣺��1����C��2��4![]() ������y=
������y=![]() �еã�m=8
�еã�m=8![]()
����2��3![]() ������y=kx+6
������y=kx+6![]() �еã�2k+6=4
�еã�2k+6=4![]()
��k=��![]()
��2���ɣ�1��֪��k=��![]() ��
��
��ֱ��AB�Ľ���ʽΪy=��![]() x+6
x+6![]() ��
��
��A��6��0����B��0��6![]() ����
����
��AB=12
��AM��ֱ��
���ANM=90����
���ANM=��AOB
�֡ߡ�MAN=��BAO��
���MAN�ס�BAO��
��![]()
��OQ=AP=t��AM=2AP=2t��OA=6��OB=6![]() ��AB=12
��AB=12
��![]()
��AN=t��MN=![]() t
t
��ON=OA��AN=6��t
�ߵ�Q���N�غ�
��ON=OQ
��6��t=t
��t=3
��3���ٵ�0��t��3ʱ��QN=OA��OQ��AN=6��2t
��S=![]() QNMN=
QNMN=![]() ��6��2t��
��6��2t��![]() t=��
t=��![]() t2+3
t2+3![]() t
t
�ڵ�3��t��6ʱ��QN=OQ+NA��OA=t+t��6=2t��6
��S=![]() QNMN=
QNMN=![]() ��2t��6��
��2t��6��![]() t=
t=![]() t2��3
t2��3![]() t��
t��
����S=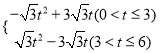



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ץס�Ļ������ڵ��̻���ij�̵��������A��B���������ڼ���Ʒ��������A�ּ���Ʒ8����B�ּ���Ʒ3������Ҫ950Ԫ��������A�ּ���Ʒ5����B�ּ���Ʒ6������Ҫ800Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2�������̵�������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ���8 000Ԫ����ô���̵������A�ּ���Ʒ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������Ϊ50�������У����ݵ����ֵ��123����Сֵ��45����ȡÿ���յ�ֵ�����ֵ�IJ�Ϊ10������������Է֣�������
A.5���6��
B.6���7��
C.7���8��
D.8���9��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015�����������ֵ��GDP����6280��Ԫ����ȫ���ŵ�21������ɽ���ŵ�3����6280�ÿ�ѧ��������ʾΪ�� ��
A.62.8��102
B.6.28��103
C.0.628��104
D.6.28��102
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������֮һ��ʹƽ���ı���ABCD�����ε�Ϊ�� ��
��AC��BD���ڡ�BAD=90�㣻��AB=BC����AC=BD��
A.�٢�
B.�ڢ�
C.�ۢ�
D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ���ADΪ����������ADEF��ʹ��DAF=��BAC������CF��
��1����ͼ1������D���߶�BC��ʱ����֤��BD=CF��
��2����ͼ2������D���߶�BC���ӳ����ϣ��ҡ�BAC=90��ʱ��
���ʣ�1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
���ӳ�BA��CF�ڵ�G������GE����AB=2![]() ��CD=BC�������GE�ij���
��CD=BC�������GE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�������ڽǡ�A=30�㣬��B=70��������ABC��( )
A. ��������� B. ֱ�������� C. �۽������� D. ����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com