
【题目】.如图,点A、B在⊙O上,直线AC是⊙O的切线,OD⊥OB,连接AB交OC于点D.
⑴求证:AC=CD
⑵若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.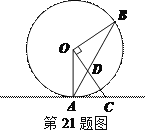
【答案】⑴证明:∵AC是⊙切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠OAB+∠CAB=90°.
∵OC⊥OB,
∴∠COB=90°,
∴∠ODB+∠B=90°.
∵OA=OB
∴∠OAB=∠B,
∴∠CAB=∠ODB.
∵∠ODB=∠ADC,
∴∠CAB=∠ADC
∴AC=CD.
⑵解:在Rt△OAC中,OC=![]() =3
=3
∴OD=OC-CD=OC-AC=3-2=1
【解析】
试题(1)由AC为圆的切线,利用切线的性质得到∠OAC为直角,再由OC与OB垂直,得到∠BOC为直角,由OA=OB,利用等边对等角得到一对角相等,再利用对顶角相等及等角的余角相等得到一对角相等,利用等角对等边即可得证.
(2)由ODC=OD+DC,DC=AC,表示出OC,在直角三角形OAC中,利用勾股定理即可求出OD的长.
试题解析:(1)∵OA=OB,∴∠OAB=∠B.
∵直线AC为圆O的切线,∴∠OAC=∠OAB+∠DAC=90°.
∵OB⊥OC,∴∠BOC="90°." ∴∠ODB+∠B=90°.
∵∠ODB=∠CDA,∴∠CDA+∠B=90°.
∴∠DAC=∠CDA. ∴AC=CD.
(2)在Rt△OAC中,AC=CD=2,AO=![]() ,OC=OD+DC=OD+2,
,OC=OD+DC=OD+2,
根据勾股定理得:OC2=AC2+AO2,即(OD+2)2=22+(![]() )2,
)2,
解得:OD=1(负值已舍去).


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于一次函数:![]() 的说法错误的是( )
的说法错误的是( )
A.它的图象与坐标轴围成的三角形面积是![]()
B.点![]() 在这个函数的图象上
在这个函数的图象上
C.它的函数值![]() 随
随![]() 的增大而减小
的增大而减小
D.它的图象经过第一、二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
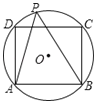
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,弦CD交AB于E,连接OD、PC、BC,∠AOD=2∠ABC,∠P=∠D,过E作弦GF⊥BC交圆与G、F两点,连接CF、BG.则下列结论:①CD⊥AB;②PC是⊙O的切线;③OD∥GF;④弦CF的弦心距等于![]() BG.则其中正确的是( )
BG.则其中正确的是( )
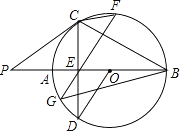
A. ①②④ B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
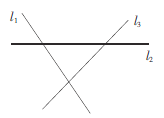
A.一处B.二处C.三处D.四处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程x2+2(m﹣1)x+m2﹣2m﹣3=0(m为实数).
(1)求证:不论m为何值,该方程均有两个不等的实根;
(2)解方程求出两个根x1,x2(x1>x2),并求w=x1(x1+x2)+x12的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
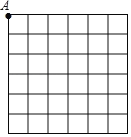
【题目】数学很酷,让我们用理性思维这一利器,去一几何的魔法世界吧.请按要求,完成下面的绘图:作图要求:①仅使用无刻度直尺:②要构造的点必须是格点.
具体要求:
(1)在如图6×6网格中,构造所有等腰三角形,其中个点为A,且一条边长为![]() ;符合条件的三角形有 个,在图上标出.
;符合条件的三角形有 个,在图上标出.
(2)简述构造长度为![]() 的线段的理论依据及计算过程.
的线段的理论依据及计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,连接
,连接![]() .下列结论中:①
.下列结论中:①![]() ;②
;②![]() 是等边角形:③
是等边角形:③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
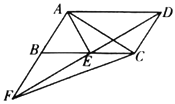
A.②③⑤B.①④⑤C.①②③D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com