
【题目】已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
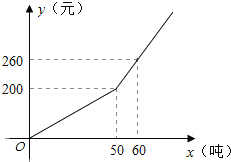
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;
(3)为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收![]() 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.
【答案】(1)y=kx+b(2)120吨(3)100吨
【解析】
试题分析:(1)设y关于x的函数关系式y=kx+b,代入(50,200)、(60,260)两点求得解析式即可;
(2)把y=620代入(1)求得答案即可;
(3)利用水费+污水处理费=600元,列出方程解决问题.
解:(1)设y关于x的函数关系式y=kx+b,
∵直线y=kx+b经过点(50,200),(60,260)
∴![]()
解得![]()
∴y关于x的函数关系式是y=6x﹣100;
(2)由图可知,当y=620时,x>50,
∴6x﹣100=620,
解得x=120.
答:该企业2013年10月份的用水量为120吨.
(3)由题意得6x﹣100+![]() (x﹣80)=600,
(x﹣80)=600,
化简得x2+40x﹣14000=0
解得:x1=100,x2=﹣140(不合题意,舍去).
答:这个企业2014年3月份的用水量是100吨.


科目:初中数学 来源: 题型:
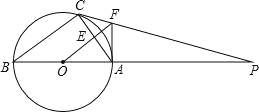
【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算:①x2+x4=x6 ②2x+3y=5xy ③x6÷x3=x3 ④(x3)2=x6,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.

(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式能用平方差公式计算的是( )
A. (3a+b)(a﹣b) B. (3a+b)(﹣3a﹣b) C. (﹣3a﹣b)(﹣3a+b) D. (﹣3a+b)(3a﹣b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的网格中,把一个点先沿水平方向平移丨a丨格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移丨b|格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的点,我们把这个过程记为(a,b)例如在图1中.从A到B记为:A→B(+1,+3)从c到D记为:C→D(+3,一3),请回答下列问题:
(1)如图1,若点A的运动路线为:A→B→D→A,请计算点A运动过的总路程;
(2)若点A运动的路线依次为:A→M(+2,+3)A→N(+1,―1),N→P
(-2,+2)P→Q(+4,—4)请你依次在图2上标出点M,N,P,Q的位置.
(3)在图2中,若点A经过(m,n)得到点E,点E再经过(p、,q)后得到Q,则m与p满足的数量关系是___________;n与q满足的数量关系是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com