
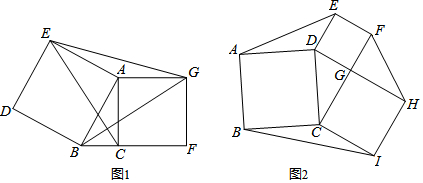
分析 (1)易证∠EAC=∠BAG,即可证明△EAC≌△BAG,可得CE=BG,∠AEC=ABG,即可证明CE⊥BG;
(2)先判断出∠EAH=∠BAC,从而△EHA≌△BCA,即可得出EH=BC,最后用三角形的面积公式计算即可得出结论;
(3)由(2)结论得出S△BCI=S△CDG,S△ADE=S△CDG,而△CDG和△FGH面积相等,最后用求得七部分面积的和即可.
解答 解:(1)线段CE和BG的数量及位置关系:CE=BG,CE⊥BG.
证明:∵∠EAB=∠GAC=90°,
∴∠EAC=∠BAG,
在△EAC和△BAG中,
$\left\{\begin{array}{l}{EA=BA}\\{∠EAC=∠BAG}\\{AC=AG}\end{array}\right.$,
∴△EAC≌△BAG(SAS),
∴CE=BG,∠AEC=ABG,
∵∠AEC+∠APE=90°,∠APE=∠BPC,
∴∠BPC+∠ABG=90°,
∴CE⊥BG;
(2)如图1,过点E作EH⊥AG交GA延长线于H,
∴∠EHA=∠90°=∠BCA,
∵∠EAH+∠BAH=90°,∠BAC+∠BAH=90°,
∴∠EAH=∠BAC,
在△EHA和△BCA中,
$\left\{\begin{array}{l}{∠EHA=∠BCA}\\{∠EAH=∠BAC}\\{AE=AB}\end{array}\right.$,
∴△EHA≌△BCA(AAS),
∴EH=BC,
∵S△ABC=$\frac{1}{2}$AC×BC=$\frac{1}{2}$AC×EH,S△AGE=$\frac{1}{2}$AG×EH=$\frac{1}{2}$AC×EH,而AC=AG,
∴△ABC与△AEG面积相等.
故答案为:S△ABC=S△AEG;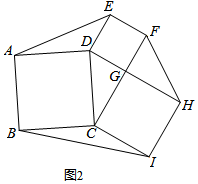
(3)如图2,∵四边形ABCD,CIHG、GFED均为正方形,∠CGD=90°,
∴CG=GH=4,DG=FG=3,△CDG与△HGF全等,
同(2)的方法可得,S△BCI=S△CDG,S△ADE=S△CDG
∴S六边形ABIHFE
=S正方形ABCD+S△BCI+S正方形CIHG+S△FGH+S正方形DEFG+S△ADE+S△CDG
=S正方形ABCD+S△CDG+S正方形CIHG+S△FGH+S正方形DEFG+S△CDG+S△CDG
=S正方形ABCD+S正方形CIHG+S△FGH+S正方形DEFG+3S△CDG
=CD2+CG2+$\frac{1}{2}$GH×FG+DG2+3×$\frac{1}{2}$CG×DG
=52+42+$\frac{1}{2}$×4×3+32+3×$\frac{1}{2}$×4×3
=25+16+6+9+18
=74(m2).
故答案为:74m2.
点评 此题属于四边形的综合题,主要考查了全等三角形的判定和性质,同角的余角相等,三角形的面积公式,正方形的面积公式的综合应用,解本题的关键是作辅助线构造全等三角形,运用等底等高的三角形面积相等,得出S△ABC=S△AGE.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.
如图,已知点A、D、B、E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.请你判断上面这个判断是否正确,如果正确,请给出说明;如果不正确,请添加一个适当条件使它成为正确的判断,并加以说明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
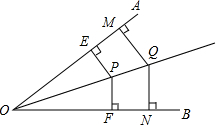 如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.
如图,P是∠AOB内部的一点,PE⊥OA,PF⊥OB垂足分别为E,F.PE=PF.Q是OP上的任意一点,QM⊥OA,QN⊥OB,垂足分别为点M和N,QM与QN相等吗?请证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com